Вопрос №2.7. Объясните физический смысл формулы полной вероятности

Объясните физический смысл формулы полной вероятности.

Ответ:

Формула полной вероятности является следствием обеих основных теорем — теоремы сложения вероятностей и теоремы умножения вероятностей.

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий:

Н1, Н2, …, Нп,.

образующих полную группу (несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них) несовместных событий (несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе). Будем эти события называть гипотезами.

Так как гипотезы Н1, Н2, …, Нп образуют полную группу, то событие, А может появиться только в комбинации с какой-либо из этих гипотез:

А=Н1•А+Н2•А+…+Нп•А Так как гипотезы Н1, Н2, …, Нп несовместны, то и комбинации Н1•А+Н2•А+…+Нп•А также несовместны. Применяя к ним теорему сложения вероятностей (Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р (А+В)=Р (А)+Р (В)), получаем:

Р (А)= Р (Н1•А)+Р (Н2•А)+…+Р (Нп•А)=.

Применяя к событию Рi•А теорему умножения (Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место: Р (А•В)=Р (А)•Р (В/А)), получим:

Р (А)= Р (Н1)•Р (А/Н1)+Р (Н2)•Р (А/Н2)+…+Р (Нп)•Р (А/Нп).

или.

Полученная формула и есть формула полной вероятности.

Пример. Вдоль линии электропередач (ЛЭП) происходит три грозовых разряда. Вероятность попадания в ЛЭП первого грозового разряда равна 0.4; второго — 0.5; третьего — 0.7. ЛЭП выходит из строя при одном попадании молнии с вероятностью 0.2; при двух попаданиях с вероятностью 0.6 и при трёх попаданиях с вероятностью 1.0.

Найти вероятность того, что в результате грозовых разрядов ЛЭП вышла из строя.

Решение. Рассмотрим четыре гипотезы:

• 1. Н0 — в ЛЭП не попало ни одного грозового разряда;
• 2. Н1 — в ЛЭП попал один разряд молнии;
• 3. Н2 — в ЛЭП попало два разряда молнии;
• 4. Н3 — в ЛЭП попало три разряда молнии.

Очевидно, что эти гипотезы имеют место при следующих сочетаниях событий, образующих несколько несовместных вариантов:

;

;

;

.

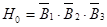
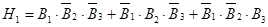
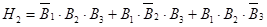
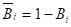
где В1, В2, В3 — попадание молнии в ЛЭП при первом, втором и третьем грозовом разряде, соответственно. — события противоположные событиям В1, В2, В3 соответственно, вычисленные как .

Пользуясь теоремами сложения, умножения и свойством противоположных событий, находим вероятности этих гипотез.

Условные вероятности события, А (выход из строя ЛЭП) при этих гипотезах равны:

;; ;

Применяя формулу полной вероятности, получаем:

Р (А)= Р (Н0)•Р (А/Н0)+Р (Н1)•Р (А/Н1)+Р (Н2)•Р (А/Н2) +Р (Н3)•Р (А/Н3)=.

0.09 •0+0.36•0.2+0.41•0.6+0.14•1.0=0.458.

Из результатов расчёта видно, что первую гипотезу Н0 можно было бы не рассматривать, так как соответствующий член в формуле полной вероятности обращается в нуль. Так обычно и поступают при применении формулы полной вероятности, рассматривая не полную группу несовместных гипотез, а только те из них, при которых данное событие возможно.

Данный пример наглядно показывает область применения формулы полной вероятности, с помощью которой можно определить вероятность некоторого события, которое может произойти вместе с одним из событий, образующих полную группу несовместных событий.

Формула полной вероятности играет большую роль при анализе надёжности сложных схем, поскольку позволяет свести любую сложную схему к совокупности элементарных. Метод оценки надёжности, основанный на формуле полной вероятности, достаточно удобен, прост и нагляден в расчётах даже без применения ЭВМ относительно небольших по объёму схем с небольшим числом ветвей и узлов, к которым можно отнести схемы внутризаводского электроснабжения.