Методика организации экскурсий математического содержания в начальной школе

Цель развивающего этапа эксперимента — увеличить уровень заинтересованности к математике через проведение уроков-экскурсий для становления познавательного интереса младших школьников. На формирующем этапе эксперимента участвовали учащиеся 4 класса.

На первых этапах изучения математики в начальной школе особенно важно больше внимания уделять вопросу выделения математических фактов из реального мира. Когда-то древний человек начал отмечать общие свойства, форму и количество, отношения и зависимости предметов и их групп. Галилею принадлежат слова: «Природа говорит языком математики: буквы этого языка — круги, треугольники и иные математические фигуры». [6, с. 94]. Но сегодня неоправданно мило используется этот огромный образовательный потенциал. Если взрослые, педагоги не создадут соответствующие условия ученикам, не предоставят им шанс «поискать математические факты вокруг себя (в том, что сотворила природа, что сделано человеком), то мало кто из детей заметит их и проявит к ним интерес.

Часто ли люди, проживающие много лет в одном доме и подъезде, знают, сколько там ступенек? Можно, конечно, сказать, что в этом нет необходимости, поэтому никто и не подсчитывает их количество. Данный пример подчеркивает, что наше внимание избирательно, и если его не направлять на что-то специально, это «что-то» можно не заметить. Мы должны научить современных учеников внимательно вглядываться в окружающий мир.

В предисловии к книге Я. И. Перельмана «Занимательная геометрия» Б. А. Кордемский утверждает, что люди, которые обучались геометрии только у классной доски, «не привыкли замечать знакомые геометрические отношения в окружающем нас мире вещей и явлений, не приучались пользоваться приобретенными геометрическими знаниями на практике в затруднитиалных случаях жизни». [4, с. 7].

Поучительны и слова М. Пруста: «Настоящее путешествие в открытие состоит не в том, чтобы стремиться находить все новые пейзажи, а в том, чтобы уметь, по-новому увидеть то, что окружает нас». Для этого крайне важно задавать ученикам очень простой, но, как показывает практики, очень действенный вопрос: «Что вы видите?» Обязательно следует дать детям время еще раз посмотреть вокруг, надо также выслушать всех, кто желает чтото сказать. В результат ученики, дополняя друг друга. перечислят многое из того, что они как бы впервые увидели. Учитель должен принимать все версии, а ученики сами спорят друг с другом, если какие-то из них не правдоподобны. Появившуюся во время наблюдения точку зрения ученику часто необходимо аргументировать. К аргументации его подтолкнет вопрос учителя: «Что вы видите здесь такого, что позволяет вам так считать?» (Этот вопрос часто применяется в образовательной технологии «Образ и мысль».).

В результате у детей развиваются мышление и речь. Таким образом, можно реализовать не только развивающий эффект, но и исследовательский подход при изучении математики и индивидуализацию учебного процесса. Каждый ученик сделает вклад в ход урока в силу своих индивидуальных особенностей (не только по уровню, но и по стилю, способностям и склонностям, исходя из имеющегося жизненного опыта и т. д.).

Расширение собственного чувственного опыта всех одноклассников, приоритет субъективного опыта взаимодействия ребенка с окружающей средой позволят каждому из них более осмысленно усваивать программный материал. Установлено, что сфера познавательных интересов младших школьников непосредственно связана с природой, явлениями естестествознания. Поэтому для изучения математики полезны экскурсии, yустанавливающие межпредметные связи с соответствующими учебными дисциплинами.

Такие связи повышают мотивацию изучения математики и расширяют детский кругозор. Знакомство с математическими сторонами жизни взрослых людей, также способствует формированию мотивации, интереса изучению математики. Особенно это касается посещения рабочих мест родителей. Дети очень гордятся такими уроками, ощущают личную причастность к математике и получают дополнительную возможность общения с отцом и матерью. Конспекты уроков-экскурсий по математике в приложении.

Цель анализа опытно-экспериментальной работы: выявить у учащихся изменения в уровнях сформированности познавательного отношения к математике.

С этой целью были проведены те же диагностические процедуры, что и на констатирующем этапе: модифицированная диагностика «Методика с конвертами» Г. И. Щукиной и «Оценка уровня сформированности учебно-познавательного интереса» Г. В. Репкиной, Е. В. Заика.

Как и на констатирующем этапе, сначала был проведен лабораторный эксперимент с использованием модифицированной диагностики «Методика с конвертами» Г. И. Щукиной, позволивший выявить группы учащихся с различным характером познавательных интересов к предмету на конец опытно-экспериментальной работы.

Результаты представлены в таблице 1.

Таблица 1 — Характер познавательного интереса у учащихся на контрольном этапе.

Учащихся с отсутствием познавательного отношения к математике выявлено не было. Учащихся с аморфными и широкими интересами, одним из которых является интерес к изучению математики, — 4 человека (28,5%) и 6 человек (43%) соответственно. Стержневой интерес к изучению математики у 4 человек (28,5%) в классе.

Обобщенные данные о характере познавательного интереса у учащихся по диагностике Г. И. Щукиной «Методика с конвертами» на конец опытно-экспериментальной работы представлено на рисунке 1.

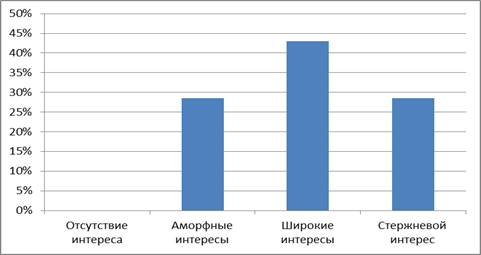
Рисунок 1. Характер познавательного интереса у учащихся на контрольном этапе.

Анализ полученных данных показывает, что на контрольном этапе опытно-экспериментальной работы (по сравнению с констатирующим) преобладают широкие интересы у учащихся, одним из которых является интерес к изучению математики (43%), отсутствие интереса к математике у учащихся не выявлено.

Изменения в характере познавательного интереса учащихся на констатирующем и контрольном этапах исследования представлены на рисунке 2.

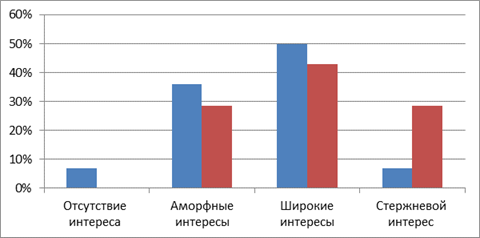
Рисунок 2. Изменения в характере познавательного интереса у учащихся.

Анализ полученных данных свидетельствует, что на контрольном этапе исследования учащихся с отсутствием интереса к математике не было выявлено, это на 7% меньше, чем было выявлено на констатирующем этапе. Кроме того учащихся с широкими интересами, одним из которых является интерес к изучению математики и учащихся с аморфными интересами, стало меньше на 7% и 7,5% соответственно. Количество учащихся со стержневым интересом к математике стало больше на 21,5%.

Таким образом, у учащихся наблюдается укрепление познавательного отношения к математике, которое проявлялось в их деятельности в процессе выполнения заданий.

Характер выбора конверта стал преобладать нацеленный, быстрый. Эмоциональный фон деятельности был увлеченный, уверенный. Даже если возникали затруднения у учащихся со стержневым интересом к изучению математики или широкими интересами, то они все равно выполняли задания до конца, хоть это и требовало большего напряжения умственной деятельности и длительного времени, При этом учащиеся выбирали исследовательские, поисковые и творческие задания.

Уровни развития познавательного интереса у учащихся были выявлены при помощи проведения диагностической методики «Оценка уровня сформирозанности учебно-познавательного интереса» Г. В. Репкиной и Е. В. Заика. Результаты отражены в таблице 2.

Таблица 2 — Уровни становления познавательного интереса учащихся на контрольном этапе.

учащийся экскурсия математика внешкольный На контрольном этапе отсутствия интереса у учащихся не выявлено. Второй уровень развития познавательного интереса (реакция на новизну) выявлен у одного учащегося (7%). Число учащихся с третьим и четвертым уровнем развития познавательного интереса составили по 28,5%. Устойчивый учебно-познавательный интерес выявлен у 22% учащихся, а высший уровень его развития — у 14%.

Обобщенные данные об уровнях развития познавательного интереса у учащихся представлены на рисунке 3.

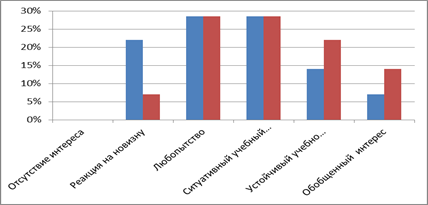
Рисунок 3. Изменение уровней развития познавательного интереса у учащихся (констатирующий и контрольный этап).

Полученные данные свидетельствуют о том, что у учащихся произошли положительные изменения уровней развития познавательного интереса — количество учащихся с устойчивым и обобщенным познавательным интересом повысилось на 8% и 7% соответственно.

Итак, по результатам двух диагностик можно сделать вывод, что наблюдается положительное изменение уровня сформированности познавательного отношения к математике у учащихся в экспериментальном классе, а, следовательно, активизации познавательного интереса у младших школьников на уроках математики с помощью экскурсий. Таким образом, данные проведенной опытно-экспериментальной работы подтвердили заявленную гипотезу о том, что активизация познавательного иинтереса у младших школьников при помощи экскурсий будет осуществляться более успешно, если учитель:

• — учитывает уровень сформированости познавательного интереса;
• — использует в процессе организации и в содержании экскурсий нестандартные методы и приемы (мини-соревнования, составление задач на местном материале);
• — проводит послеэкскурсионную работу по использованию полученных на экскурсиях знаний.

Выводы по II главе

Таким образом, для того, чтобы приблизить обучение к реальности, нужно рассматривать территориальные особенности в постижении разных дисциплин исходной школы. Математические уроки-экскурсии дают огромные вероятности для организации разных видов деятельности учащихся, в итоге которых они постигают свой родной край.

Основная задача математических экскурсий заключается в том, дабы формировать у учащихся приемы умственных действий, находить математику вокруг себя, расширить познания учеников. При планировании экскурсии для школьников младшего школьного возраста следует руководствоваться тем, что у них больше развита наглядно-образная память, у старших словесно-логическая. Дети младшего возраста лучше, стремительней запоминают и крепче сберегают в памяти определенные, блестящие факты и события.

Если применение экскурсий как формы организации обучения сделать больше систематическим, то это дозволит повысить интерес к предмету, улучшит усвоение учебного материала, будет содействовать возрастанию уровня математических умений учащихся.