Эмпирическое исследование развития самостоятельности при решении текстовых задач в 3 классе

Выявление уровня сформированности самостоятельности на уроках математики Опытно-экспериментальная работа проводилась в течение четырех недель и состояла из 16 уроков математики. В исследовании приняли участие учащиеся третьих классов: контрольный 3 «в» (20 обучающихся, из которых — 12 девочек, 8 мальчиков) и экспериментальный 3 «а» (20 обучающихся, из которых — 11 девочек, 9 мальчиков). Возраст детей располагается в рамках 8,5- 9 лет.

Важнейшее условие получения достоверных результатов — это установление эмоционального контакта и взаимопонимания между двумя сторонами эксперимента. Для этого необходимо проводить исследование в привычной для обучающихся обстановке. Соблюдать условия, при которых класс не испытывает отрицательных эмоций (страх, неуверенность).

Исследование предполагало прохождение трех основных этапов:

• 1 этап — констатирующее исследование, предполагающее диагностику уровня сформированности самостоятельности у детей обоих классов;
• 2 этап — формирующее исследование, а именно работа учеников только 3 «а» класса над текстовыми задачами;
• 3 этап — контрольное исследование — повторная диагностика уровня сформированности самостоятельности у обучающихся обоих третьих классов и выявление разницы.

Для подтверждения выдвинутой гипотезы нами были использованы следующие методы исследования:

• — анализ философской, психологической и педагогической литературы по исследуемой проблеме;
• — методы психолого-педагогической диагностики (тестирование, метод математической статистики);
• — обобщение и систематизация педагогического опыта.

На констатирующем этапе эксперимента с целью выявления исходного уровня сформированности самостоятельной учебной деятельности учащихся была использована диагностика параметров самостоятельной деятельности младших школьников, разработанная Н. В. Калининой (далее Диагностика — 1). Учащимся предлагалась анкета, вопросы которой были направлены на изучение таких параметров, как: успеваемость, мотивация, активность, организованность, ответственность и самостоятельность. Каждый вопрос имел три варианта ответа, учащимся необходимо было выбрать один ответ и отметить его знаком «+». После суммирования баллов, полученных каждым учеником, определялись уровни сформированности самостоятельной учебной деятельности:

Высокий уровень (8−12 баллов) — успеваемость ученика отличная или хорошая, учащийся проявляет устойчивый учебно-познавательный интерес к самостоятельной работе, инициативу, если требуется выполнить нестандартное упражнение, выполняет самостоятельную работу без помощи учителя, умеет организовать свое рабочее место, планировать время и способы действия при выполнении самостоятельной работы.

Средний уровень (4−7 баллов) — успеваемость ученика хорошая или средняя, учащийся проявляет ситуативный учебно-познавательный интерес к самостоятельной работе, инициативу; если требуется выполнить доступные задания, требующие размышления, выполняет самостоятельно только задания средней сложности, умеет организовать свое рабочее место, планировать время и способы действия при выполнении самостоятельной работы.

Низкий уровень (0−3 балла) — успеваемость ученика низкая, учащийся не проявляет интерес к самостоятельной работе, выполняет самостоятельно без помощи учителя только задания репродуктивного характера, не умеет организовать свое рабочее место, планировать время и способы действия при выполнении самостоятельной работы.

Далее ученикам третьих классов мы предложили решить задачу:

В книжном шкафу было 120 книг. Когда детям выдали книги, в шкафу осталось 56 книг. На сколько больше книг выдали, чем осталось?

Данная диагностика была необходимо для определения уровня сформированности умения самостоятельно решать текстовые задачи (далее Диагностика-2). Основные критерии представлены в таблице № 2.

Таблица № 2.

Уровни сформированности умения решать текстовые задачи определялись в соответствии с набранными баллами.

Высокий уровень (13−18 баллов): при полном всестороннем анализе задачи обучающийся способен выделить целостную систему взаимосвязей между величинами, видит основные данные, что позволяет ему осуществлять целостное планирование решения задачи, используя разные способы. Решает задачу без помощи учителя.

Средний уровень (8 -12 баллов).

Восприятие задачи сопровождается ее анализом. Обучающийся стремится выделить данное и искомое, но не способен воссоздать единую схему, что затрудняет прогноз последующего хода решения задачи. Ученик осуществляет пошаговое планирование.

Низкий уровень (0 — 7 баллов). Восприятие задачи осуществляется учеником поверхностно, неполно.

Результаты диагностик представлены в таблице № 3.

Таблица № 3.

Из таблицы видно, что в экспериментальном 3 классе по Диагностике-1 20% учащихся имеют высокий уровень сформированности самостоятельности, у 45% школьников выявлен средний уровень и у 35% выявлен низкий уровень сформированности самостоятельности. Близкие результаты в экспериментальном классе дает Диагностика-2. В контрольном третьем классе по Диагностике-1 10% учащихся имеют высокий уровень сформированности самостоятельности, у 50% детей выявлен средний уровень и у 40% выявлен низкий уровень сформированности самостоятельности. Аналогичные результаты применительно к контрольному классу дает Диагностика-2.

Мы можем сделать вывод, что необходимо уделять больше внимания самостоятельной работе учеников на уроках математике.

Формирующая работа по развитию самостоятельности посредством решения текстовых задач На формирующем этапе эксперимента нами были разработаны и реализованы на уроках математики в экспериментальном 3 классе разноуровневые задания для самостоятельных работ с текстовой задачей, направленные на повышение уровня самостоятельности и дифференцированные задания для работы с текстовой задачей для разных групп учащихся. Задания составлены в соответствии с изучаемыми разделами курса математики в 3 классе (УМК «Школа России»). Разноплановые задания вводились поэтапно и предлагались для выполнения отдельным ученикам, группе учащихся или всему классу.

1. Задачи, направленные на раскрытие смысла арифметических действий.

Каждая из этих задач вводится в то время, когда программой предусмотрено ознакомление с соответствующими действиями (сложение, вычитание, умножение, деление).

2. Задачи, раскрывающие различные отношения между числами.

В начальном курсе математики особенно много внимания уделяется работе над отношениями между числами, которые могут быть выражены словами «быть равными», «быть на столько-то больше (меньше), чем», «быть во столько-то раз больше (меньше)».

Данные задачи могут быть представлены в прямой и косвенной формах:

• — В задачах, выраженных в прямой форме, если содержится выражение «на (во) столько-то (раз) меньше», т. е. требуется узнать меньшее число, используется действие вычитание (деление); если содержится выражение «на (во) столько — то (раз) больше» — используется сложение (умножение).
• — В задачах, выраженных в косвенной форме, при встрече с выражением «на (во) столько-то (раз) больше», используется действие вычитание (деление), если же содержится выражение «на (во) столько — то (раз) меньше» — используется сложение (умножение).
• 3. Задачи, раскрывающие связи между компонентами и результатами арифметических действий.

Это задачи на нахождение одного из компонентов действия, когда даны другой компонент и результат.

• 4. Задачи, связанные с понятиями доли, дроби числа.
• 5. Задачи, в которых раскрывается зависимость между величинами.

Связи между пропорциональными величинами раскрываются с помощью решения простых задач на нахождение одной из величин по данным, соответствующим значениям двух других величин.

Данные текстовые задачи использовались из сборников упражнений А. Е. Захаровой, С. В. Нерсесова, А. О. Самсонова, В. Н. Студенецкой. Отобранные нами задачи классифицированы в таблице № 4.

Таблица № 4.

карандашей в коробке?

3+4=7 (шт.). 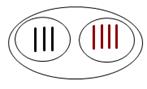Ответ: 7 карандашей в коробке.

карандашей в коробке? 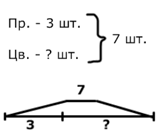7−3=4 (шт.). Ответ: 4 цветных карандаша в коробке.

7−4=3 (шт.). Ответ: 3 простых карандаша в коробке.
Нахождение разности (остатка).	Нахождение неизвестного уменьшаемого.	Нахождение неизвестного вычитаемого.
Мама купила 7 пирожных. 3 пирожных съели. Сколько осталось? Было — 7 п. Съели — 3 п. Осталось —? п. 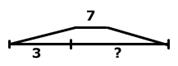7−3=4 (п.). Ответ: 4 пирожных осталось.	Мама купила пирожные. После того, как 3 съели, осталось 4. Сколько пирожных купили? Было —? п. Съели — 3 п. Осталось — 4 п. 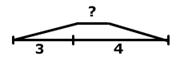3+4=7 (п.). Ответ: 7 пирожных купили.	Мама купила 7 пирожных. После того, как несколько съели, осталось 4. Сколько пирожных съели? Было — 7 п. Съели —? п. Осталось — 4 п. 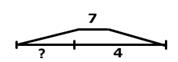7−4=3 (п.). Ответ: 3 пирожных съели.
Увеличение на несколько единиц.	Уменьшение на несколько единиц.	Разностное сравнение.
В коробке лежало 3 простых карандаша, а цветных на 2 больше. Сколько цветных карандашей лежало в коробке?	В коробке лежало 5 цветных карандашей, а простых на 2 меньше. Сколько простых карандашей лежало в коробке?	В коробке лежало 5 цветных и 3 простых карандаша. На сколько больше было цветных карандашей, чем простых?
3+2=5 (шт.). Ответ: 5 цветных карандашей лежало в коробке.	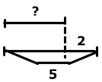5−2=3 (шт.). Ответ: 3 простых карандаша лежало в коробке.	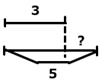5−3=2 (шт.). Ответ: на 2 цветных карандаша больше, чем простых.
Могут быть представлены в прямой и косвенной формах.
Нахождение произведения.	Нахождение неизвестного множителя.	Нахождение неизвестного множителя.
На каждой тарелке по 3 груши. Сколько груш на четырех тарелках? 1 способ: 3+3+3+3=12 (гр.) 2 способ: 3?4=12 (гр.). 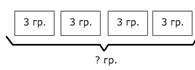Ответ: 12 груш на четырех тарелках.	Цена открытки 3 Сколько открыток купить на 12 рублей? 12:3=4 (шт.). Ответ: 4 открытки купить на 12 рублей.	рубля. можно можно.	За 4 одинаковые открытки заплатили 12 рублей. Узнай цену открытки? 12:4=3 (руб.). Ответ: 3 рубля стоит одна открытка.
Нахождение частного.	Нахождение неизвестного делимого.	Нахождение неизвестного делителя.
Деление на равные части.	Задумали число. После того,.	После того, как число 10.
	как его.	разделили.	на 5,.	разделили на неизвестное.
	получили.	2. Какое.	число.	число, получили 2. Найдите.
6 яблок.	разложили на 3.	задумали?	делитель.
тарелки.	поровну. Сколько.
яблок положили на каждую.	х:5=2.	10:х=2.
тарелку?	х=2*5.	х=10:2.
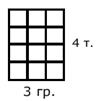6:3=2 (ябл.). Ответ: 2 яблока на каждой тарелке. Деление по содержанию. На конверты наклеили 6 марок: по 2 марки на каждый конверт. Сколько получилось конвертов с марками? 6:2=3 (к.). Ответ: 3 конверта с марками.	х=10.	х=5.
	10:5=2.	10:5=2.
	2=2 (верно).	2=2 (верно).
	Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.	Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
Увеличение в несколько раз.	Уменьшение в несколько раз.	Кратное сравнение.
У Васи было 3 карандаша, а у Пети в 2 раза больше. сколько карандашей у Пети?

У Пети было 6 карандашей, а у Васи в 2 раза меньше. сколько карандашей у Васи?

У Васи было 3 карандаша, а у Пети 6. Во сколько раз больше карандашей у Пети, чем у Васи?

одного такого пакета.

пакетов потребуется, чтобы разложить в них поровну 8 кг муки?

8:2=4 (шт.). Ответ: 4 пакета потребуется.
Нахождение доли (дроби) от числа.	Нахождение числа по его доли (дроби).
От ленты, длиною 15 метров отрезали третью часть. Сколько метров отрезали? 15:3=5 (м) Ответ: 5 м ленты отрезали.	От ленты отрезали третью часть, равную 5 метрам. Какова длина всей ленты? 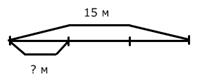5?3=15 (м) Ответ: 15 м длина всей ленты.

Формирование навыков самостоятельного решения текстовых задач проходило поэтапно. На первом этапе младшие школьники учились выполнять учебные задания на основе образца. Вторая стадия отражала формирование среднего уровня учебной самостоятельности (операционные действия). На этом этапе младшие школьники учились встраивать способ действия (анализ, синтез, классификация) в учебную деятельность, применять его в дальнейшем на новом материале.

Повторная диагностика уровня сформированности самостоятельности младших школьников Основной целью контрольного этапа эксперимента стало определение эффективности предложенного нами комплекса разноуровневых заданий. Для этого мы повторно провели в обоих третьих классах Диагностику-2, описанную в разделе 3.1 (задача была изменена). Полученные результаты представлены в диаграмме № 1 и № 2.

Диаграмма № 1.

Диаграмма № 2.

Результаты повторной диагностики показали, что в экспериментальном 3 классе самостоятельная учебная деятельность сформирована: на высоком уровне? у 30% учащихся, на среднем уровне? у 60% учащихся на низком уровне? у 10% учащихся. Наблюдается положительная динамика. А в контрольном 3 классе, где дополнительная работа по развитию самостоятельности не проводилась, уровень самостоятельности учебной деятельности остался практически прежним: на высоком уровне? у 25% учащихся, на среднем уровне? у 45% учащихся на низком уровне? у 25% учащихся. Мы можем сделать вывод, что предложенные нами разноуровневые и дифференцированные задания при систематическом использовании ведут к положительной динамике в процессе формирования умения самостоятельно решать задачи. Кроме того, для формирования самостоятельности при решении текстовых задач на уроках математики мы предлагаем использовать памятку с перечислением ошибок, возникающих при работе над текстовыми задачами, разработанную на основе трудов Б. П. Есипова.

Выводы по главе III.

В экспериментальной части исследования был определен уровень сформированности самостоятельности младших школьников. Разработаны и апробированы разноуровневые задания для самостоятельных работ на уроках математики с учетом уровня сформированности навыков самостоятельного решения текстовых задач. Была отслежена динамика уровня сформированности самостоятельности младших школьников экспериментального класса.

В результате проведенного эксперимента была отмечена положительная динамика уровней сформированности самостоятельности младших школьников экспериментального класса, что служит доказательством эффективности разработанных и реализованных разноуровневых текстовых задач для самостоятельной работы на уроках математики в начальной школе.