Некоторые приемы и методы решения логических задач

Развивающие логические задачи для учеников 5−6 классов целесообразно подбирать так, чтобы в ходе их решения происходило постепенное освоение приемов и методов решения алгебраических и геометрических задач, широко применяемых в старших классах.

Доказательство от противного. Доказать справедливость утверждения «от противного», значит предположить противное и путем логических высказываний прийти к противоречию с условием, что доказывает неверность высказанного предположения.

1. Доказать, что из натуральных чисел от 1 до 100 нельзя выбрать 71 число таким образом, что бы их сумма равнялась сумме остальных чисел.

Решение: сумма всех натуральных чисел от 1 до 100 равно5050, а сумма 71 из них не меньше, чем 1+2+3+…+71=2556. Но число 2556 больше половины от 5050. Следовательно, требуемые 71 число выбрать нельзя.

2. Витя сказал своему другу Коле: «Я придумал пример на деление, в котором делимое, делитель, частное и остаток оканчиваются соответственно на 1, 3, 5 и 7». Подумав, Коля ответил: «Что-то ты путаешь». Прав ли Коля?

Решение. Предположим, что такой пример на деление существует. Тогда делимое a, делитель b, частное q и остаток r — нечетные числа. Но из равенства a=bq+r следует, что a — четное число. Полученное противоречие доказывает неверность высказанного предположения. Значит, Коля прав.

Принцип Дирихле — это утверждение, согласно которому в любой совокупности из n множеств, содержащих в общей сложности n+m элементов, есть хотя бы одно множество, содержащее не менее двух элементов. Принцип Дирихле часто применяется при решении математических задач. Основная идея решения задач такова, что если при разбиении множества на непересекающиеся части удается установить взаимосвязь между количеством элементов множества (N) и числом его частей (n) в виде N > n, то тогда можно утверждать, что среди этих частей есть такая, которая содержит более одного элемента.

• 1. В коробке лежат карандаши: 4 красных и 3 синих. В темноте берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее одного синего? (5)
• 2. В школе 370 учеников. Найдутся ли в этой школе хотя бы два ученика, у которых день рождения приходится на одну и ту же дату календаря? (да)

Контр пример и подтверждающий пример. Чтобы убедиться в ложности высказывания, необходимо привести пример, для которого заданное свойство не выполняется. Чтобы доказать истинность высказывания, необходимо указать хотя бы один пример, для которого заданное свойство выполняется.

• 1. Верно ли, что если произведение двух натуральных чисел больше 100, то каждое число больше 10? (нет, 52и 3)
• 2. Можно ли треугольник разрезать так, чтобы получились 3 четырехугольника? (да)

Рассмотрение крайних случаев. Смысл приема заключается в том, чтобы на основе изучения поведения исследуемого объекта в крайних или предельных случаях, исходя из наибольших или наименьших значений, выявить области поиска решения задачи. Или рассматривается самый худший случай, в котором утверждение задачи кажется наиболее невыполнимым. Если в худшем случае утверждение верно, то во всех остальных ситуациях тем более верно.

1 (6 класс). Из цифр 1, 2, 3, 4 составили два четырехзначных числа с различными цифрами. Доказать, что ни одно из них не делится на другое.

Решение. Наибольшее число, которое может быть составлено из цифр 1, 2, 3, 4 при условии, что цифры в записи числа не повторяются, равно 4321, а наименьшее — 1234. Отсюда, если бы одно из составленных чисел делилось бы на другое, отличное от первого, то в частном получилось бы либо 3, либо 2. Но сумма цифр составленных чисел равна 1 + 2 + 3 + 4 = 10 и не делится на 3, поэтому в частном не может быть 3. В частном не может быть и 2, так как при умножении числа, составленного из цифр 1, 2, 3, 4 на 2 получается число, составленное из цифр 2, 4, 6, 8, что противоречит условию. Следовательно, данное в задаче утверждение справедливо.

2. (5 класс) Вова утверждал, что в этом году будет месяц с пятью воскресеньями и пятью средами. Прав ли он? (нет).

Перебор — проведение определенным образом организованного перебора и анализа всех случаев, которые потенциально возможны в ситуации, описанной в задаче.

• 1. Сколько имеется двузначных чисел, у которых а) среди цифр есть хоть одна пятерка? б) цифра десятков меньше цифры единиц? в) цифра десятков больше цифры единиц? (а)18; б)36; в) 45)
• 2.) Количество учащихся одной из школ выражается трехзначным числом. Если найти сумму цифр этого числа, затем сумму цифр полученного числа, то все эти числа можно записать так: АВА, ВС, В, где одинаковые буквы обозначают одинаковые цифры. Сколько учеников в этой школе?(В = 2, ВС = 20, АВА = 929)
• 3. Лиса наловила 28 окуней и разложила их в 7 кучек так, что во всех кучках было разное число рыб. Попробуйте и вы так разложить. (1 + 2 + 3 + 4 + 5 + 6 + 7 =28)
• 4. Напишите девять цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9. Не меняя порядка этих цифр, расставьте между ними плюсы и минусы, всего три знака, таким образом, чтобы в результате получилось 100.
• (123 — 45 -67 + 89 =100)
• 5. Если между числами двузначного числа поставить цифру 2, то получится трехзначное число, равное квадрату исходного. Найдите это число. (11, т.к. 11²=121)

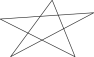
• 6. Сколько четырехугольников в пятиугольной звезде? (5)
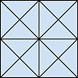
• 7. В одном квадрате спрятались 44 треугольника. Найди их.

Перефразирование. При решении задачи с использованием этого приема, необходимо перейти к равносильной путем перевода текста исходной задачи на другой язык (например, с естественного на символический) или нахождения новой интерпретации заданных условий в рамках одного и того же языка. Такой перевод лежит в основе алгебраического метода решения текстовых задач, заключающегося в составлении уравнения, неравенства, системы уравнений или системы неравенств.

Приём получения следствий состоит в том, что раскрытие содержания исходных данных даёт возможность получить некоторые выводы, а из полученных результатов — новые выводы и т. д. Нередко таким способом удаётся найти решение предложенной задачи.

1. Сколько всего прапрабабушек и прапрадедушек было у всех Ваших прапрабабушек и прапрадедушек?

Решение: Так как у каждого человека было 8 прабабушек и 8 прадедушек, а у каждого из этих 16 человек также было по16 прямых предков в «четвёртом колене», то искомое число равно 1616 = 256.

2. Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равны делимое, делитель, частное?

Решение: Делимое в 6 раз больше делителя означает, что частное равно 6. Отсюда, если частное равно 6, а делитель в 6 раз больше частного, то делитель равен 36. Окончательно получаем, что делимое равно 36?6=216.

Метод «проб и ошибок» — эвристический прием, который используется в тех ситуациях, когда у решающего нет более конструктивных идей. Прежде чем добиться искомого результата, необходимо отвергнуть массу неудачно выбранных действий, отказаться от каких-то вариантов и вновь вернуться к ним и, как правило, случайный успех позволяет нащупать верное решение.

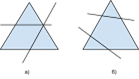
1. Проводя 2 прямые, разделите треугольник на: а) два треугольника и один четырёхугольник; б) два треугольника, один четырёхугольник и один пятиугольник.

2. Как разрезать на две части прямоугольник со сторонами 4 см и 9 см так, чтобы из них можно было сложить квадрат?