Примеры задач разных этапов математической олимпиады

Решение: Покажем, что математики могли выбрать число; это число является корнем уравнения. Ясно, что. Нетрудно видеть, что при натуральных мы имеем, где и — целые числа, причем при нечетных и при четных. Значит, число иррационально. Осталось показать, что для любого натурального числа сумму в рублей можно набрать требуемым способом. Рассмотрим все способы набрать n рублей выпущенными монетами… Читать ещё >
Примеры задач разных этапов математической олимпиады (реферат, курсовая, диплом, контрольная)
В данной работе подробно рассмотрена методика организации и проведения математических олимпиад на разных этапах, а также рассмотрены основные особенности олимпиад. Обязательным требованием, предъявляемым к заданиям этих олимпиад, является нестандартность и их новизна для участников. При переходе к каждому последующему этапу олимпиады увеличивается сложность заданий. Чтобы в этом убедится, рассмотрим примерные задачи 3 этапов олимпиады для учащихся 10 классов (задания для школьного этапа олимпиады составляют школьные учителя).
II этап (муниципальный).
1. Вася, Петя и Миша стартовали одновременно в забеге на 1 км. Когда Вася финишировал, Петя отставал от него на 100 м, а Миша отставал от Пети на 90 м. Петя закончил бег на 18 секунд позже Васи. На сколько секунд позже Пети прибежал Миша? (Известно, что скорость каждого была постоянной на протяжении всей дистанции).
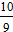
Решение: Когда Вася финишировал, Петя пробежал 900 м, а Миша 810 м, то есть скорость Пети в раз больше скорости Миши. Это означает, что когда Петя закончит бег (то есть пробежит 1000 м), Миша пробежит 900 м. То есть за 18 секунд Миша пробежит 900 810 = 90 м. Значит, его скорость равна 5 м/с, и оставшиеся 100 м он пробежит за 20 секунд.
Ответ: На 20 секунд.
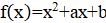
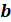
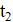
2. Приведённый квадратный трёхчлен имеет два корня. Докажите, что если вычесть из коэффициента любой из этих корней, а коэффициент удвоить, то полученное уравнение также будет иметь корень.
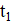
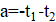
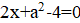
Решение: Согласно теореме Виета, если и — корни данного уравнения, то,. Поэтому новое уравнение имеет вид. Дискриминант этого уравнения равен. Значит, у этого уравнения есть корень.
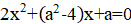
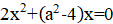
10.3.. Имеется таблица 1111. Двое играют в следующую игру. Они по очереди ставят в пустые клетки этой таблицы крестики и нолики: первый за ход ставит один крестик, а второй — один нолик. Игра заканчивается, когда все клетки таблицы заполнены. После этого вычисляются два числа: A — количество строк, в которых больше крестиков, чем ноликов, и B — количество столбцов, в которых больше ноликов, чем крестиков. Первый выигрывает, если A > B, иначе выигрывает второй. Кто выигрывает при правильной игре?
Решение: Заметим сначала, что в каждой строке и каждом столбце по 11 клеток; поскольку число 11 нечётно, в каждом из этих рядов крестиков и ноликов не может быть поровну. Приведем выигрышную стратегию для первого игрока. Сначала ему нужно поставить крестик в центральную клетку таблицы. Каждым следующим ходом ему следует ставить крестик в клетку, симметричную относительно центра таблицы клетке, в которую только что поставил нолик второй игрок (понятно, что он всегда сможет так сделать). Покажем, что при такой стратегии количество строк, в которых больше крестиков, будет больше количества столбцов, в которых больше ноликов. Заметим, что все клетки таблицы (кроме центральной) разобьются на пары симметричных относительно центра, причём в каждой такой паре клеток будут стоять ровно один нолик и один крестик. Рассмотрим сначала среднюю строку таблицы. В центральной клетке (центре таблицы) стоит крестик. Остальные 10 клеток разбиваются на 5 пар симметричных. Это означает, что в них стоят 5 крестиков и 5 ноликов. Значит, всего в этой строке стоят 6 крестиков и 5 ноликов, поэтому в центральной строке крестиков больше, чем ноликов. Аналогично, в центральном столбце крестиков больше, чем ноликов. Рассмотрим теперь первую и последнюю строки таблицы. Их клетки образуют 11 пар симметричных клеток. Это означает, что в них суммарно стоит 11 крестиков и 11 ноликов. Значит, если в одной из этих строк больше крестиков, то в другой больше ноликов. Аналогичное утверждение можно доказать про остальные пары симметричных строк 51 таблицы, а также про все пары симметричных столбцов. Итак, в этих парах количество строк, в которых больше крестиков, будет равно 5, и количество столбцов, в которых больше ноликов, будет также равно 5. Поэтому A= 6, B = 5, и первый выиграет.
Ответ: Выигрывает первый.
III этап (региональный).
1. Натуральное число n умножили на сумму его цифр и получили 1000. Найдите все такие числа n.
Решение: Раскладывая 1000 в произведение двух множителей: 1000×1, 500×2, 250×4, 200×5, 125×8, 100×10, 50×20, 40×25 мы получаем два варианта ответа.
Ответ: 125 и 1000.
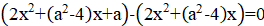
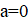
2. При каких значениях параметра уравнения и будут иметь общий корень? Найдите корень.
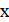
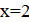
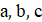
Решение: Если — корень уравнения, то он также и корень уравнения, то есть. Кроме того, по условию, — корень уравнения. Значит — корень уравнения, то есть. Осталось проверить, что при таких оба уравнения имеют общий корень.
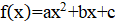
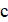
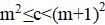
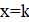
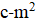
Ответ:, .
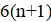
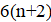
3. Коэффициенты квадратного трёхчленанатуральные числа, сумма которых равна 2000. Паша может изменить любой коэффициент на 1, заплатив 1 рубль. Докажите, что он может получить квадратный трёхчлен, имеющий хотя бы один целый корень, заплатив не более 1050 рублей.
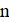
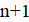
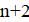
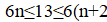
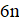
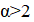
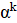
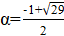
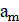
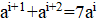
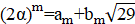
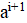
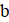
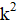
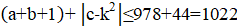
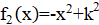
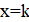
Решение: Покажем, что можно из исходного трёхчлена получить новый, имеющий хотя бы один целый корень, изменив коэффициенты суммарно даже не более, чем на 1022. Если коэффициент не больше 1022, то, сделав его равным нулю, мы получим искомый трёхчлен, имеющий целый корень. Пусть теперь; тогда из условия. Рассмотрим два последовательных квадрата, между которыми находится:. Поскольку, имеем. Тогда одна из разностей и не превосходит, то есть она не больше. Итак, найдется натуральное число, для которого. Заменив теперь на -1, на 0, а на, мы изменим коэффициенты суммарно не более, чем на, и получим трехчлен, имеющий целый корень .
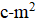
IV этап (заключительный).
1. Назовём натуральное число хорошим, если среди его делителей есть ровно два простых числа. Могут ли 18 подряд идущих натуральных чисел быть хорошими?
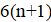
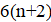
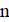
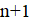
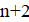
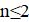
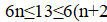
Решение: Предположим, что нашлись 18 хороших чисел подряд. Среди них найдутся три числа, делящихся на 6. Пусть это числа, и. Поскольку эти числа — хорошие, и в разложение каждого из них на простые множители входят двойка и тройка, других простых делителей у них быть не может. Далее, лишь одно из трёх подряд идущих натуральных чисел, , может делиться на 3. Значит, остальные два являются степенями двойки. Но пары степеней двойки, отличающихся не более чем на два — это только (1, 2) и (2, 4); поэтому. Однако тогда среди наших 18 чисел есть простое число 13 (так как)), не являющееся хорошим. Противоречие.
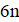
Ответ: Не могут.
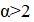
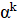
2. В республике математиков выбрали число и выпустили монеты достоинствами в 1 рубль, а также в рублей при каждом натуральном. При этом б было выбрано так, что достоинства всех монет, кроме самой мелкой, иррациональны. Могло ли оказаться, что любую сумму в натуральное число рублей можно набрать этими монетами, используя монеты каждого достоинства не более 6 раз?
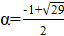
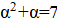
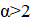
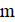
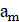
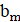
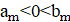
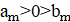
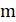
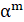
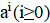
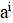
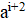
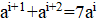
Решение: Покажем, что математики могли выбрать число; это число является корнем уравнения. Ясно, что. Нетрудно видеть, что при натуральных мы имеем, где и — целые числа, причем при нечетных и при четных. Значит, число иррационально. Осталось показать, что для любого натурального числа сумму в рублей можно набрать требуемым способом. Рассмотрим все способы набрать n рублей выпущенными монетами (хотя бы один такой способ существует: можно взять рублёвых монет). Выберем из них способ, в котором наименьшее число монет. Предположим, что какая-то монета достоинства встречается в этом способе хотя бы 7 раз. Тогда можно заменить 7 монет по монетами достоинств и. При этом суммарное достоинство монет не изменится (поскольку), а их количество уменьшится. Это невозможно по выбору нашего способа. Итак, этот способ удовлетворяет условию.
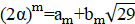
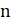
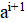
Ответ: Могло.
5. Анализ результатов 57 областной олимпиады школьников по математике (2−3 февраля 2015 года) (III этап Всероссийской математической олимпиады школьников) В нашей области ежегодно проводятся три тура олимпиад: школьный, районный (городской), областной, что способствует выявлению одаренных и талантливых учащихся, имеющих интерес и склонности к занятию математикой. На первом этапе участвуют все желающие учащиеся 5−11 классов, на втором — учащиеся 6−11 классов (победители первого тура), на третьем учащиеся 9−11 классов (победители второго тура, набравшие не менее половины необходимых баллов).
Тексты заданий для проведения второго и третьего тура олимпиады разрабатываются и утверждаются областным оргкомитетом. При подготовке заданий третьего тура учитываются рекомендации центральных предметных комиссий.
2−3 февраля 2015 года проведена 57 областная олимпиада школьников по математике (региональный этап Всероссийской олимпиады школьников) на базе ГАОУ ДПО ВО «Владимирский институт развития образования имени Л.И. Новиковой».
Общие справочные данные В олимпиаде приняли участие 15 команд. Число участников составило 50 обучающихся 9−11 классов: 9 класс — 10 чел., 10 класс — 17 чел., 11 класс — 23 чел. В таблице № 1 приведен сравнительный анализ числа участников за пять лет.
Таблица 1. Сравнительный анализ участников олимпиады.
Год. | Общее число участников. | % учащихся городских школ. | Количество команд. | |
82%. | ||||
87%. | ||||
81%. | ||||
94%. | ||||
91%. | ||||
94%. | ||||
Из таблицы № 1 видно, что количество участников (9 — 11 классы) в этом году незначительно уменьшилось. Это можно объяснить тем, победители и призеры (муниципального этапа) олимпиады определялись жюри в соответствии с итоговой таблицей, рекомендованной Центральной предметно-методической комиссией по математике. Больший процент участников областной олимпиады — это ученики городских школ, что составляет 94% от общего числа участников.
Таблица 2. Победители и призеры олимпиады 2015 года.
Статус участника. | Класс. | Ф.И. участника. | Кол-во баллов. | Территория (школа). | Учитель. | |
Победитель. | ; | ; | ; | ; | ||
Призеры. | Цыбаева Александра Соснина Екатерина Аникеич Елизавета Рыбка Татьяна Ледащев Григорий. |
| МБОУ Гимназия № 1 г. Коврова МБОУ СОШ № 21г. Коврова. МБОУ СОШ № 15 г. Владимира МАОУ Гимназия № 3 г. Владимира МАОУ Гимназия № 3 г. Владимира. | Пронина Е.Б. Баранова И.А. Шавлинская Т.Ю. Большакова Г. В. Большакова Г. В. | ||
Победитель. | ; | ; | ; | ; | ||
Призеры. | Пугачева Ирина Лисенков Глеб Суслов Кирил Исмаилов Рашад. |
| МБОУ СОШ № 2 г. Гусь-Хрустальный МБОУ СОШ № 2 г. Гусь-Хрустальный МБОУ СОШ № 6 г. Вязники МБОУ СОШ № 2 г. Гусь-Хрустальный. | Баженова Н.В. Баженова Н.В. Вожжаниковова М.А. Баженова Н.В. | ||
Победитель. | ; | ; | ; | ; | ||
Призеры. | Ященко Тимур Юлегин Павел. |
| МБОУ СОШ № 7 г. Кольчугино МБОУ СОШ № 13 г. Александров. | Волокитина Ю.С. Милькевич Н.В. | ||
В таблице 2 указаны призеры регионального этапа олимпиады по математике и учителя, подготовившие данных учеников (по итогам олимпиады в 2015 г. победителей нет). Призеры 11 класса Татьяна Рыбка и Григорий Ледащев являлись призерами олимпиады и по результатам олимпиады 2014 года в 10 классе. Призеры 10 класса Ирина Пугачева и Рашад Исмаилов являлись призерами олимпиады и в прошлом году в 9 классе. Следует отметить, что 55% от числа призеров 9−11 классов проходили обучение в интеллектуальной школе олимпийского резерва (ИШОР) на базе ГАОУ ДПО ВИРО на очной сессии (осень 2014 г.).
В этом году результаты олимпиады в 11 классе оказались ниже в сравнении с прошлыми годами. Победитель не определен (набрано менее 50% баллов). Наивысший результат призера 17 баллов из 56 возможных (победитель в 2014 году — 29 баллов, в 2013 году — 35 баллов).
Еще ниже результаты показали и учащиеся 9 классов. Призер Ященко Тимур набирает всего 18 баллов из 56 возможных баллов. Отмечаем, что в 2014 г. и 2013 г. был аналогичный показатель (победитель не определился, а призер получил соответственно 20 и 23 балла).
Следует заметить, что победителями и призерами регионального этапа олимпиады (анализ анкет участников олимпиады) становятся учащиеся из профильных классов и школ, где математика изучается в большем объеме, а также школьники, посещающие факультативные или индивидуальные занятия под руководством учителя, при этом, акцент в организации учебных занятий переносится на освоение способов учебной деятельности, умение осуществить поиск способа решения задачи, формирования умения оперировать усвоенными знаниями и умениями в новой ситуации.
Отмечаем, что 22% участников (11 человек из 50 участников регионального этапа олимпиады) — это участники ИШОР и из них 45% стали призерами. Остальные ребята, обучающиеся школы олимпийского резерва набрали количество баллов близкое к баллам призеров, что говорит о качественной подготовке и об эффективной работе данной школы.
Ежегодно стабильные результаты показывают команды образовательных учреждений г. Владимира, г. Вязники, г. Гусь-Хрустальный, г. Коврова, г. Кольчугино и это не случайно, так как в образовательных учреждениях данных территорий учителями математики ведется серьезная подготовительная работа к математическим олимпиадам, что ежегодно подтверждают результаты регионального этапа Всероссийской олимпиады школьников по математике.
Двух призеров (11 класс) подготовила учитель математики МАОУ Гимназия № 3 г. Владимира Г. В. Большакова и трех призеров (10 класс) подготовила учитель математики МБОУ СОШ № 2 г. Гусь-Хрустальный Н. В. Баженова.
Анализ качества практической подготовки школьников Региональный этап Всероссийской олимпиады школьников проводится по заданиям, подготовленным Центральной предметно-методической комиссией (председатель Н.Х. Агаханов). Олимпиада проходила в два этапа и участникам предлагалось выполнить 8 задач:
- 1 этап (02.02.2015) — учащимся было предложено 4 задачи;
- 2 этап (03.02.2015) и участникам необходимо было выполнить еще 4 задачи.
Каждая задача оценивалась максимально в 7 баллов. Максимальное количество баллов составило — 56.
Таблица 3. Анализ результатов по классам.
Класс. | Кол-во участ-ников. | Макси-мальный балл. | Верхний предел балльной оценки участников олимпиады. | Нижний предел балльной оценки участников олимпиады. | Средний балл участников олимпиады. | ||||
2015 г. | 2015 г. | 2015 г. | 2014 г. | 2015 г. | 2014 г. | 2015 г. | 2014 г. | ||
7,5. | |||||||||
9,4. | |||||||||
Анализируя результаты по классам (таблица № 3), видим, что средний балл значительно возрос у участников в 9 классе. Резко снизился средний балл как в 11 классе (с 10 до 7), так и в 10 классе (с 11 до 9,4). Следует отметить, что наблюдается снижение среднего балла в 10 и 11 классах в течение трех последних лет. Верхний предел балльной оценки во всех классах стал ниже, особенно это заметно в 11 классе (с 29 до 17 баллов), что составляет 30% от возможного максимального балла. Лучший результат по сравнению с 9 и 11 классами показали участники в 10 классе, наибольший балл — 22, что составляет 39% от возможного максимального балла. Нижний предел балльной отметки незначительно вырос в 9 и 10 классе.