Квадратичные формы и главные компоненты

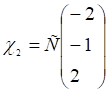
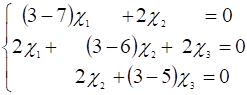
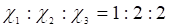
Для того чтобы представить в геометрическом плане главные компоненты, рассмотрим простейшие случаи: плоскости и пространства трех измерений.

Пусть дано уравнение линии второго порядка:

Ах2 +2Вху + Су2 =Н. (13).

Левая часть уравнения (13) не меняется при замене х, у нах, -у. Значит, во-первых, точки линии (13) расположены парами симметрично относительно начала координат. Во-вторых, линия второго порядка, заданная (13), обладает центром симметрии и, в-третьих, начало координат помещено в центр. Левая часть (13) представляет собой однородный многочлен второй степени. Такой многочлен называют квадратичной формой от двух переменных.

Ах2 +2Вху + Су2 (14).

Приведем данную квадратичную форму (14) к каноническому виду. Для этого надо будет повернуть так координатные оси х и у, чтобы в новых координатах исчез член с произведением новых текущих координат. Переход к новым координатам производится по известным формулам:

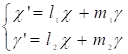
(15).

Старые координаты связаны с новыми по формулам:

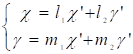
(16).

где х' и у' - новые координаты.

Характеристика коэффициентов со старыми координатами представлена на рис. 1.

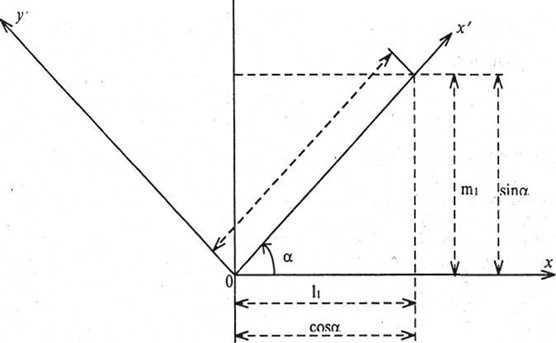
Рис. 1 Единичный вектор и его компоненты

На рис. 1 на новой оси абсцисс отложен отрезок ОХ1 единичной длины, тогда его проекции на старые координатные оси составят:

где б — угол поворота осей х и у.

Значит, вектор с компонентами l1 и m1 является единичным вектором, определяющим направление новой оси абсцисс х':

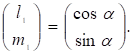
(18).

Аналогично единичный вектор, определяющий направление новой оси у' ординат, имеет вид:

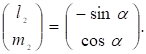
(19).

Чтобы привести квадратичную форму (14) к каноническому виду, нужно в (14) величины х и у заменить согласно формуле (16). Квадратичная форма примет вид:

. Ах2 + 2Вху + Су2 =лхх'2+л2у'2. (20).

Для решения (20) достаточно подобрать так коэффициенты (16) и числа л1, л2, чтобы.

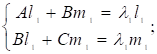
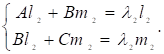
Значит, надо решить систему уравнений.

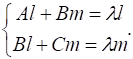
(21).

В системе (21) перенесем правые части влево и получим.

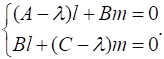
(22).

Определитель данной системы.

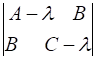
=0. (23).

можно представить в виде.

(24).

Откуда.

(25).

Уравнение (23) представляет собой характеристическое уравнение квадратичной формы, а корни этого уравнения л1 и л2 являются характеристическими числами этой формы. После приведения формы к каноническому виду числа л1 и л2 являются коэффициентами при неизвестных.

Так как выражение под радикалом, равное.

(А-С)2 +4В2? 0, (26).

неотрицательно, то уравнение (22) имеет только действительные корни. Отдельно рассмотрим случай, когда.

(А-С)2 +4В2>0. (27).

При этом условии л1? л2. Подставим в (21) л = л1. Система будет иметь ненулевое решение l и т.

Полученный вектор будет иметь главное направление квадратичной формы, которое соответствует характеристическому числу л1.

По этому же главному направлению, которое соответствует числу л1 направлен и вектор

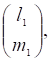
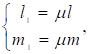
т.е. (28).

где µ?0.

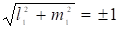
Если примем, что, то по системе (28) .

Вектор является единичным вектором главного направления.

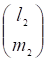
Векторопределяет другое главное направление квадратичной формы.

Если л1? л2, векторы главных направлений взаимно перпендикулярны.

Другой случай соответствует.

(А-С)2 + АВ2 = 0. (29).

В данном случае.

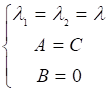
. (30).

Из выражения (25).

л = А = С.

Подставим в выражение (24) полученное значение л и убедимся в том, что все коэффициенты системы обращаются в нуль. Таким образом, система (22) будет состоять из тождеств. Ей подходят любые числа l и т.

В результате можно заключить, что если л1 = л2, то для квадратичной формы любое направление является главным. При повороте осей на любой угол форма сохранит свой канонический вид Ах2 + Ау2.

При любом преобразовании квадратичной формы к любым прямоугольным координатам не меняются ее инварианты.

. (31).

Согласно теореме Виета.

АС-В2= л1 л2. (32).

1. Если л1? 0; л2? 0 имеют одинаковые знаки, то квадратичная форма называется эллиптической:

АС-В2>0. (33).

2. Если л1? 0; л2? 0, но знаки у них разные, то форма называется гиперболической:

АС-В2<0. (34).

3. Если одно из чисел л1, л2 равно нулю, т. е. АС-В2 =0, то форма называется параболической.

В методе главных компонент характеристические числа по своему физическому смыслу не могут равняться нулю и быть отрицательными. Значит, л1>0 и л2 >0. В этом случае квадратичная форма будет называться положительно определенной эллиптической формой.

На рис. 2 показаны переход от произвольной системы координат к системе с точкой нуль в центре эллипса и поворот осей, осуществленный для приведения квадратичной формы к каноническому виду. После приведения к каноническому виду ось абсцисс, соответствующая л1, направлена по одной главной оси эллипса (главному направлению), а ось координат, соответствующая другому главному направлению, направлена перпендикулярно к ней вдоль другой главной оси эллипса. Вдоль главной оси эллипса оу направлена первая главная компонента, а вдоль оси ох направлена вторая главная компонента.

Рис. 2 Перенос системы координат (х, 0, у) в центр эллипса и поворот на угол б

На рис. 2 первое главное направление (у') определяется л1, а второе главное направление (х') определяется характеристическим числом л2 .