Основные определения и факты

Ценные бумаги, фигурирующих на финансовом рынке, делятся на два основных класса: рисковые и безрисковые активы. Все разновидности безрисковых активов ведут себя приблизительно как банковский счёт. Рисковые же активы эволюционируют как акции и имеют ярко выраженный случайный характер. Такая двойственность и легла в основу математического названия финансового рынка-(B, S)-рынка. Прежде чем дать строгое определение этому понятию, рассмотрим две последовательности: и .

Нижние индексы обозначают дискретные моменты времени, причёмэто начальный момент времени, с которого на финансовом рынке производятся определённые действия, подвергаемые анализу, афинальный (терминальный) момент времени, на котором этот анализ завершается.

Первая последовательностьэто последовательность положительных чисел, которые отражают эволюцию цены единицы банковского счёта.

Приведём наиболее общепринятые формулы эволюции банковского счёта. Обозначим через процентную ставку, приведенную по отношению к определенному временному периоду (год, месяц, день, час и т. д). Эволюция банковского счёта по формуле простых процентов происходит следующим образом:

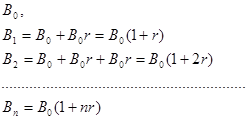
В этом случае проценты начисляются исходя только из начальной суммы, а процентные деньги в дальнейшем увеличении капитала не участвуют.

Формула сложных процентов.

В этой формуле проценты начисляются с суммы начального капитала и процентных денег:

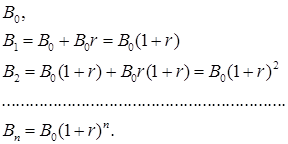
В основном в учебном пособии используется формула сложных процентов для банковского счета. Формула сложных процентов может быть записана в виде разностного уравнения:

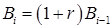
.(1.1).

В формуле (1.1) проявляется смысл процентной ставки. Процентная ставка по банковскому счету — это отношение наращенного капитала или прибыли:, к капиталу: .

Последовательность представляет собой последовательность случайных векторов цен акций разного типа:

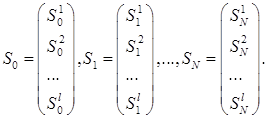
Нижний индекс по-прежнему рассматривается как момент времени, в который происходит изменение цен акций, а верхний отражает тип акции.

Так как цены акций изменяются случайным образом, то естественно считать, что они представляют собой случайные величины на некотором вероятностном пространстве (Щ, F, P). Мы будем предполагать, что пространство элементарных событий Щ-конечное множество, а элементы множества Щ будем трактовать как состояния финансового рынка. Под F будем понимать у-алгебру всех подмножеств Щ и каждое событие из F будем трактовать как событие, могущее произойти на финансовом рынке. Так как F конечно, то для неё понятие у-алгебра совпадает с понятием алгебра событий.

Для акций можно ввести понятие процентной ставки, также как это делается для банковского счета:

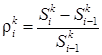
, (1.2).

В отличие от банковского счета — случайные величины, определенные на том же вероятностном пространстве, что и стоимости акций. Если известно.

.

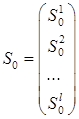
то последовательность.

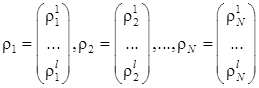
полностью определяет последовательность случайых векторов .

Определение 1.1.

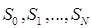
(B, S)-рынком называется объект, состоящий из детерминированной последовательности строго положительных чисел, интерпретируемых как цены банковского счёта в моменты времени 0,1,2,…, N (цены безрисковых активов), и последовательности неотрицательных случайных векторов на конечном вероятностном пространстве (Щ, F, P), интерпретируемых как цены акций в моменты времени 0,1,2,…, N. (цены рисковых активов).

Определение 1.2.

Портфелем ценных бумаг (или финансовой стратегией называется объект.

.

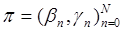
состоящий из последовательности случайных величин где каждое интерпретируется как число единиц банковского счёта в момент времени n, и последовательности случайных векторов.

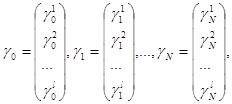
где каждое интерпретируется как число акций k-го типа в момент времени n (k=1,2,…, l; n=0,1,2,…, N). Последовательности и определены на том же самом вероятностном пространстве.

Определение 1.3.

Полным капиталом портфеля р в момент времени n (n=0,1,2,…, N) называется случайная величина.

.

где понимается как скалярное произведение (n=0,1,2,…, N). Причём не обязаны быть целыми и неотрицательными, у банка берётся заём. Предполагается, что единица банковского счета — безгранично делима. Аналогичное предположение справедливо для .

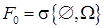
Будем считать, что для момента времени нам известны все события, которые могут произойти до момента включительно. Обозначим черезалгебру этих событий. Таким образом, возникает неубывающая последовательностьалгебр:. Обычно считается, что — тривиальная алгебра, состоящая из двух элементов всего и пустого множества —, то есть; финальнаяалгебра — .

Определение 1.4.

Неубывающая последовательностьалгебр событий называется фильтрацией (или информационным потоком). Объект (Щ, полученный из вероятностного пространства после внедрения в него фильтрации, называется стохастическим базисом.

Поскольку в момент времени нам становится известным цены акций, то естественно считать, что случайный вектор определен наалгебре, То есть последовательность является согласованной или адаптированной. Аналогичное можно сказать относительно последовательности процентных ставок .

Рассмотрим промежуток времени [n-1,n). Момент — момент объявления новых цен акций. В этот промежуток времени мы перераспределяем капитал портфеля между акциями и банковским счетом и получаем в результате единиц банковского счёта и акций. В результате возникает уравнение.

.(1.3).

Выполняя это действие, мы опираемся на информацию доступную до момента времени включительно, это означает, что и определены наалгебре, то есть предсказуемы. В момент времени в результате объявления новых цен полный капитал портфеля, как уже отмечалось ранее,.

(1.4).

где.

.

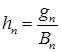
такое переобозначение будет удобным в последствие. Если, то капитал портфеля определяется только стоимостью акций и банковского счета в момент времени (самофинансируемый портфель); если, то часть средств, полученных от реализации акций и банковского счета, изымается (портфель с потреблением; если, то к средствам, полученным от реализации акций и банковского счета добавляется некоторая сумма (портфель с инвестициями).

Теорема 1.1

Рассмотрим портфель ценных бумаг с капиталом (1.4) и распределением (1.3). Тогда следующие условия равносильны:

• (b) балансовое соотношение:
• © формула приращения капитала:
• (d) формула приращения дисконтированного капитала:

.

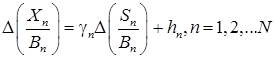
Заметим, что под дисконтированием в финансовой математике понимается отношение цен рисковых активов к цене безрискового актива.

Определение 1.5.

Финансовым обязательством[5,стр.17] называется произвольная неотрицательная случайная величина.

Экономически финансовое обязательство-это количество денег, которое мы запланировали получить в терминальный момент в результате ведения портфеля ценных бумаг.

Определение 1.6.

(B, S)-рынок называется полным[5,стр.23], если любое финансовое обязательство реплицируемо, то есть существует такой самофинансируемый портфель.

.

что его финальный капитал в точности совпадает с, то есть.

Определение 1.7.

(B, S)-рынок называется безарбитражным [5,стр.23], если не существует самофинансируемого портфеля, удовлетворяющего условиям.

и причём хотя бы одно из чисел.

Определение 1.8.

Самофинансируемый портфель называется верхним (x,)-хеджем, если он удовлетворяет условиям:

• 1)
• 2)

Совокупность всех верхних (x,)-хеджей обозначается.

Определение 1.9.

Верхней ценой [5,стр.35](стоимостью) контракта называется число.

Ш).

Определение 1.10.

Самофинансируемый портфель.

называется нижним (x,)-хеджем, если он удовлетворяет условиям:

• 1)
• 2)

Совокупность всех нижних (x,)-хеджей обозначается.

Определение 1.11.

Нижней ценой (стоимостью) контракта называется число.

Ш).

Определение 1.12.

(,)-хедж называется совершенным, если он является одновременно верхним и нижним, то есть если выполняется равенство.

Теорема 1.2.

Если данный рынок безарбитражен, то для любого финансового обязательства верно неравенство.

Теорема 1.3.

Если данный (B, S)-рынок безарбитражен и полон, то для любого финансового обязательства значения и совпадают, причём для существует совершенный (x,)-хедж.

Определение 1.13.

Пусть (Щ,-стохастический базис, а адаптированная последовательность с.в. (т.е. для любых n=0,1,…, N с.в. измерима относительно алгебры Данная последовательность с.в. называется мартингалом, супермартингалом, субмартингалом, если для любого n=0,1,…, N-1 справедливо,, соответственно. Разумеется, необходимо существование вышеуказанных условных математических ожиданий.

Приведем простой пример.

Пример 1.1. Пусть.

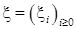
последовательность независимых одинаково распределенных случайных величин, принимающих два значения: -1 и 1 и.

.

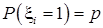
Построим последовательность частичных сумм.

.

Определим естественную фильтрацию.

.

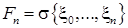
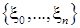
Последняя запись означает, что содержит все события, порождаемые случайным набором, например, принадлежит событие.

.

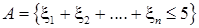
Последовательность частичных сумм — адаптированная последовательность относительно этой фильтрации. Вычислим условное математическое ожидание.

.

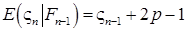
Возможны три варианта. Вариант первый,.

мартингал, вариант второй,.

— супермартингал,.

субмартингал. Важным инструментом для вычислений в стохастической финансовой математике является разложение Дуба.