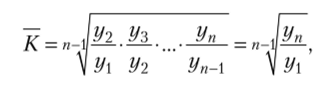Виды средних величин

В статистике выделяют следующие средние величины:

• • по наличию признака-веса:
  • а) средняя арифметическая простая,
  • б) взвешенная средняя величина.

Если имеются сведения о влиянии некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная;

• • по форме расчета:
  • а) средняя арифметическая величина,
  • б) средняя гармоническая величина,
  • в) средняя геометрическая величина,
  • г) средняя квадратическая, кубическая величина и т. д.

Средняя арифметическая простая (не взвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают через х (xj, х₂, х₃, …, х_п); число единиц совокупности обозначают через п, среднее значение признака — х. Следовательно, средняя арифметическая простая равна:

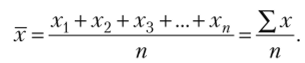
Средняя арифметическая величина — это такое среднее значение признака, при вычислении которого общий объем признака в совокупности равномерно распределяется между всеми ее единицами. Например, предположим, что на предприятии работает п работников, причем величины заработной платы любых двух работников не совпадают. Для этой совокупности можно рассчитать размер заработной платы в среднем, т. е. такую ее величину, которая приходилась бы на одного работника, если бы весь фонд оплаты труда (в данном случае это и есть общий объем признака) предприятия распределялся между всеми сотрудниками поровну.

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т. е. данные не сгруппированы. Если же данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.

Средняя арифметическая взвешенная вычисляется, но формуле.

где f_i — частота повторения г-х вариантов признака, называемая весом.

Таким образом, средняя арифметическая взвешенная равна сумме взвешенных вариантов признака, деленной на сумму весов:

В экономической практике используется широкий круг показателей, вычисляемых в виде средних величин. Наиболее простой и распространенной является средняя арифметическая. Средняя арифметическая имеет ряд свойств, знание которых упрощает ее вычисление.

1. Средняя арифметическая сумма варьирующих величин равна сумме средних арифметических величин:

Пример 2.1.

Выпускаемое изделие х состоит из двух деталей у и z, на изготовление каждой расходуется в среднем у = 3 ч, z — 5 ч.

Время на изготовление данного изделия будет равно 8 ч.

2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую сторону:

Это правило показывает, что средняя является равнодействующей.

• 3. Если все варианты ряда уменьшить или увеличить на одно и то же число, то средняя уменьшится или увеличится на это же число.
• 4. Если все варианты ряда уменьшить или увеличить в несколько раз, то средняя также уменьшится или увеличится во столько же раз.
• 5. Если все частоты ряда разделить или умножить на одно и то же число, то средняя не изменится. Это свойство показывает, что средняя зависит не от размера весов, а от соотношения между ними.

Одновременное применение различных свойств средней арифметической заметно упрощает ее расчет.

Пример 2.2.

В таблице приведены данные о дневной выработке рабочих.

Выработка деталей, шт. (х)	Число рабочих 00.
		— 10.	— 2.		— 8.

Выработка деталей, шт. (х).	Число рабочих ел.
		— 5.	— 1.		— 6.
				7,5.
		+э.	+1.		+3.
		+10.	+2.	4,5.	+9.
Итого.		;	;		— 2.

Для упрощения расчетов все варианты ряда х уменьшим на 40, а затем еще в 5 раз. Зная, что величина средней не изменится, если все частоты ряда уменьшить или увеличить в несколько раз, сократим частоты в 20 раз. Получим после этого среднюю величину:

Чтобы по этой средней исчислить среднюю первоначального ряда, необходимо умножить ее на 5 и к полученному результату прибавить 40: -0,08 • 5 + 40 = 39,6 дет.

В качестве постоянного числа а следует брать значение признака, расположенного в середине ряда или имеющего наибольшую частоту, в качестве постоянного числа А — величину интервала между признаками.

Средняя гармоническая. Средняя гармоническая тождественна средней арифметической, т. е. . Она применяется тогда, когда неизвестны действительные веса /, а известно произведение xf = 2. Для определения средней гармонической необходимо иметь ряд вариантов и частот, т. е. значения х и /. В некоторых случаях известны индивидуальные значения признака х и произведения xf, а частоты/ неизвестны. Чтобы исчислить среднюю, обозначим произведение xf = 2, откуда / = —. Теперь.

х

преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и 2 исчислять среднюю. Подставим в формулу средней арифметической вместо xfг и вместо / — —. Получим:

х

Средняя в такой форме называется средней гармонической и обозначается х_гарм.

Пример 2.3.

В таблице приведены данные об объеме производства в тыс. руб. и производительности в руб. на одного рабочего в час на трех производствах.

Применяя формулу средней гармонической взвешенной, получим:

Этот же результат мы получим и по средней арифметической взвешенной, если в качестве весов примем площадь каждого производства:

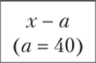
В тех случаях, когда произведения х/ одинаковы или равны единице (г = 1), применяется средняя гармоническая простая, вычисляемая по формуле.

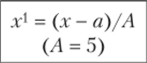
где х — отдельные варианты; п — их число.

Пример 2.4.

В бригаде работают три человека, которые производят одни и те же детали. При этом первый рабочий затрачивает на производство одной детали ½, второй 1/3, третий 1 /4 ч. Требуется определить средние затраты времени на производство одной детали. Определим их по формуле средней гармонической простой:

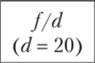
Применив среднюю арифметическую простую, мы получили бы: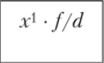

Средняя геометрическая. В некоторых случаях приходится исчислять средний коэффициент роста на единиц}' времени. Применить для этого среднюю арифметическую нельзя, так как в этом случае уравненная совокупность не будет равна первоначальной, т. е. будет нарушено определяющее свойство средних величин. Убедимся в этом.

Пример 2.5.

Приведенные в таблице коэффициенты роста выпуска продукции получены путем деления показателя выпуска каждого данного года на показатель предыдущего. Необходимо определить средний годовой коэффициент роста выпуска продукции по заводу за четыре года.

Простая средняя будет равна: х = (1,1 +1,2+1,9)/3 = 1,40. Если умножить выпуск продукции за первый год на простую среднюю, а полученный результат еще раз умножить на 1,40 и т. д. до четвертого года, то получим: 20 • 1,4 = 28,0; 28,0 -1,4 = 39,2; 39,2 • 1,4 = = 54,88, а не 50,1, как действительности, что свидетельствует о нарушении определяющего свойства средних величин.

Если в нашем примере обозначить выпуск продукции через г/, г/₂> У л* У> ежегодные коэффициенты роста — через К_х, К₂, К₃, а число коэффициентов — через и, то.

Общий коэффициент роста за изучаемый период равен:

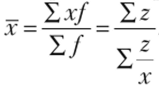
Если теперь каждый из индивидуальных коэффициентов роста заменить средним, то исходя из определяющего свойства.

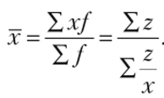
Отсюда

В нашем примере 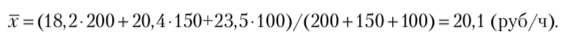Аналогично

Среднегодовой темп роста выпуска продукции на заводе за указанные годы составил 135,85%. Если теперь 20, т. е. продукцию 1-го года, умножить на среднюю геометрическую, то получим: 20? 1,3585 = 27,17; 27,17 • 1,3585 = 36,91; 36,91 • 1,3585 = 50,1. Таким образом, применение средней геометрической определяющее свойство средней не нарушает.

Итак, если имеется п коэффициентов роста, то формула среднего коэффициента роста будет иметь следующий вид:

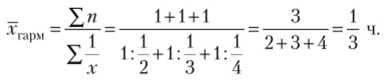
Это и есть формула средней геометрической.

Средний коэффициент роста можно определить и по данным последнего и первого уровней ряда. Если первый уровень ряда обозначить у_х, а последний — у_п, то.

где п — число дат, а не коэффициентов.

Приведенные формулы идентичны, но первая применяется в тех случаях, когда имеются текущие коэффициенты или темпы роста, а вторая — когда имеются абсолютные значения начального и конечного уровней ряда.

Средняя квадратическая. В тех случаях, когда необходимо найти среднее значение величин, выраженных в виде квадратных функций, применяется средняя квадратическая. Например, средние диаметры колес, труб, стволов, средние стороны квадратов и т. д. определяются при помощи средней квадратической.

Средняя квадратическая простая исчисляется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число:

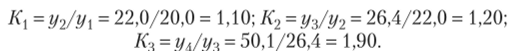
Средняя квадратическая взвешенная равна: где / — веса.

Пример 2.6.

Имеется пять квадратов со сторонами 2, 5, 6, 8, 9 м. Определим среднюю сторону квадратов:

Степенные средние. Подводя итоги, можно рассмотренные выше средние величины представить в виде формулы степенной средней вида.

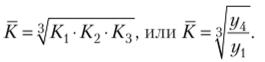
где х — средняя величина, х — индивидуальные значения признака, п — число единиц изучаемой совокупности, k — показатель степени средней.

Придавая показателю степени средней (k) различные целые значения, получим отдельные виды степени средних:

k = 1 — средняя арифметическая: 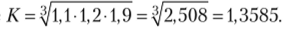k = (-1) — средняя гармоническая:

k = 2 — средняя квадратическая:

При расчете различных степенных средних по одним и тем же данным статистического наблюдения средние не будут одинаковы. Чем выше степень k средней, тем больше ее величина. Математически доказано, что между величинами степенных средних, рассчитанных, но одной и той же совокупности единиц статического наблюдения и одному и тому же признаку, существует следующее соотношение: