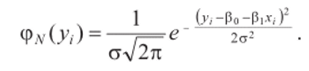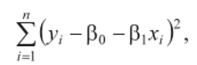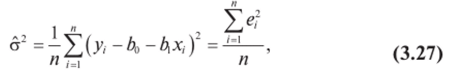Теорема Гаусса—Маркова.
Эконометрика
Что совпадает с условием (3.4) нахождения оценок />0 и Ь методом наименьших квадратов. Следовательно, оценки />0 (3.11) и Ь. Функция правдоподобия, выражающая плотность вероятности совместного появления результатов выборки, имеет вид. До сих пор мы использовали оценки параметров, полученные методом наименьших квадратов. Рассмотрим еще один. Для его применения должен быть известен вид закона… Читать ещё >
Теорема Гаусса—Маркова. Эконометрика (реферат, курсовая, диплом, контрольная)
Таким образом, оценки и Ь в определенном смысле являются наиболее эффективными линейными оценками параметров Ро И р!
До сих пор мы использовали оценки параметров, полученные методом наименьших квадратов. Рассмотрим еще один.
важный метод получения оценок, широко используемый в эконометрике, — метод максимального правдоподобия.
Метод максимального правдоподобия.
Для его применения должен быть известен вид закона распределения вероятностей имеющихся выборочных данных.
Полагая выполнение предпосылки 5 (с. 72) регрессионного анализа, т. е. н о р м, а л ь н у ю классическую регрессионную модель (3.22), будем рассматривать значения у, как независимые нормально распределенные случайные величины с математическим ожиданием М[у,)= Р"+Р,*" являющимся функцией от и постоянной дисперсией а2.
Следовательно, плотность нормально распределенной случайной величины у,
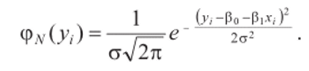
Функция правдоподобия, выражающая плотность вероятности совместного появления результатов выборки, имеет вид.
Согласно методу максимального правдоподобия в качестве оценок параметров р0, pj и ст2принимаются такие значения р0, р, и а2, которые максимизируют функцию правдоподобия L.
Очевидно, что при заданных значениях х, xiхп объясняющей переменной X и постоянной дисперсии а2 функция правдоподобия L достигает максимума, когда показатель степени при е будет минимальным по абсолютной величине, т. е. при условии минимума функции
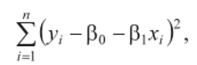
что совпадает с условием (3.4) нахождения оценок />0 и Ь методом наименьших квадратов. Следовательно, оценки />0 (3.11) и Ь
(3.13) параметров ро, pi совпадают с оценками метода максимального правдоподобия (30 и р, Для нахождения оценки ст2 максимального правдоподобия параметра а2, максимизирующей функцию L, качественных соображений уже недостаточно, и необходимо прибегнуть к методам дифференциального исчисления. Приравняв частную производную — = 0 (соответствующие выкладки предлагаем про- да1
вести читателю самостоятельно), получим.
где параметры ро и pj заменены их оценками Ьо и Ь. Сравнивая с полученной ранее несмещенной оценкой s1 (3.26), видим, что оценка а2 (3.27) метода максимального правдоподобия параметра а2 является смещенной.
В соответствии со свойствами оценок максимального правдоподобия оценки (Ьо, Ь) и су2 (а значит, и s2) являются состоятельными оценками. Можно показать, что при выполнении предпосылки 5 о нормальном законе распределения возмущения е, (/=1,…, п) эти оценки являются независимыми.