Натуральное число — мера величины

Вопросы для обсуждения.

• 1. В чем суть способа наложения для сравнения однородных величин? Почему этот способ различен для различных величин?
• 2. В чем суть операции сложения величии? Как сложить две длины, две массы, две площади? Что является результатом сложения в каждом из приведенных примеров?
• 3. В чем суть умножения величины на число? Что является результатом такого умножения?
• 4. Почему для представления скалярной величины любого рода можно и нужно использовать в качестве знаков-индексов отрезки, такие, что большей величине соответствует больший отрезок?
• 5. В чем суть измерения величин? Что является результатом измерения?
• 6. Какое свойство меры является основой операции сложения чисел — мер величины?
• 7. Какое свойство меры является основанием операции умножения чисел — мер величины?
• 8. Почему меры величин можно складывать и умножать, а величины одного рода только складывать, по не умножать?

На основе понятия положительной скалярной величины конструируется еще одна онтологически значимая модель натурального числа. К положительным скалярным величинам относятся длина, масса, продолжительность процесса, площадь и др. Несмотря на то что каждая из них является абстракцией различных свойств предметов, явлений или процессов окружающего мира, все они обладают одними и теми же математическими свойствами. А. Н. Колмогоров выделил десять свойств, определяющих понятие «скалярная величина». Они могут быть расположены по следующим группам. Группа I. Отношение сравнения

1. Любые две величины а и b одного рода можно сравнивать, получая в результате одно и только одно из отношений:

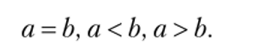
2. Отношение «<�» транзитивно:

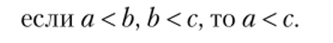
Группа II. Сложение скалярных величин.

1. Любые две величины а и Ь одного рода можно складывать, получая величину с того же рода:

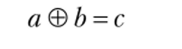
• (знак © обозначает операцию сложения величин, а не чисел; смысл операции сложения величин устанавливается для величин определенного рода свой).
• 2. Сложение величин коммутативно:

%*

3. Сложение величин ассоциативно:

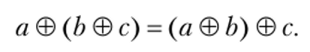
4. Сложение величин монотонно относительно отношения сравнения:

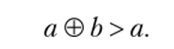
5. Если а > Ь, то определена операция вычитания а (c) b такая, что.

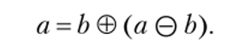
Группа III. Умножение скалярной величины на число.

Каковы бы ни были величина а и натуральное число п_у существует величина b такая, что.

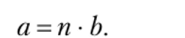
Отсюда следует, что величину можно делить на произвольное число равных частей.

Группа IV. Аксиома Архимеда

Для любых величин а и b существует такое натуральное число к, что.

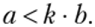
Это свойство называется аксиомой Архимеда (аксиомой Евдокса), оно означает, что какая бы ни была величина b, взятая достаточное число раз, она может превзойти любую другую фиксированную величину того же рода.

Группа V. Непрерывность скалярной величины

Если последовательности величин одного рода а_х < а₂<… 2] обладают тем свойством, что Ь_п — а_п < с для любой величины с при достаточно большом номере п_у то существует единственная величинах, которая больше всех а_п и меньше всех Ь_п.

Если какую-либо произвольную величину е взять за единичную и рассмотреть все величины я, ей кратные, то для них отношение а/е, называемое числовым значением или мерой величины а в единицах е, является натуральным числом, которое называют результатом измерения величины а единицей е. Меру а в единицах е записывают разными способами: а/е = k, а = ke, т_е(а) = к.

Теоретической основой сложения и умножения чисел — мер величины являются свойства меры: аддитивность и мультипликативность.

Аддитивность меры. Мера суммы величин равна сумме мер каждой, если величины измерены одной и той же единицей:

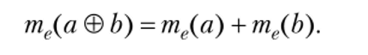
Прведем доказательство для случая мер величин — натуральных чисел.

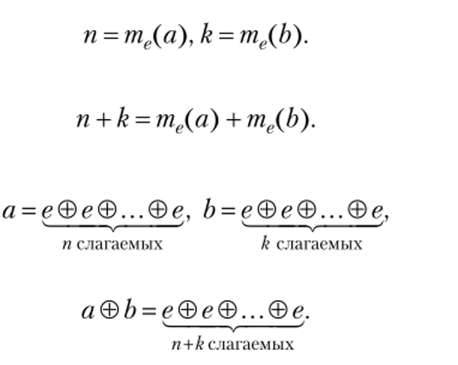
Предполагая, что рассматриваемые величины а и b кратны одной и той же величине, имеем Тогда Так как-то Одну и ту же величину можно измерять различными единицами. Свойство, которое связывает результаты таких измерений, называется свойством мультипликативности меры.

Это значит, что.

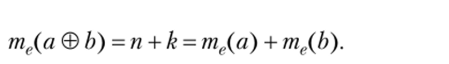
Мультипликативность меры. Если мера величины а в единицах е равна я, а мера величины е в единицах t равна к, то мера величины а в единицах t равна п • к.

Прведем доказательство для случая мер величин — натуральных чисел.

Пусть т_е(а) = т?, m_t (е) = к. Тогда получаем равенства.

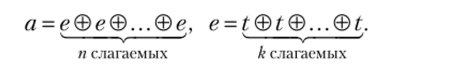
Подставляя в первое из них значение е из второго, имеем 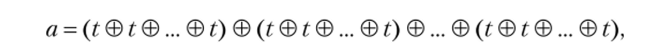где п • к слагаемых, т. е. m_t(a) = п к.

Важнейшим свойством любой скалярной величины является свойство непрерывности. Его можно пояснить так: на какие бы «мелкие» части ни «разбить» величину, каждая ее часть по-прежнему будет являться величиной того же рода. Наиболее простым наглядным объектом, относительно которого интуитивно ясно, что он непрерывен, является отрезок, точнее — его графическая модель. Поэтому скалярные величины естественно кодировать отрезком (знаками-индексами) так, что большую величину представляет больший отрезок.

Если все величины одного рода (например, массы) таковы, что их меры при выбранной единице кратны этой единице, то эти величины кодируются отрезками числового луча, один конец которого совпадает с началом луча, а второй — с точкой, определяющей второй конец отрезка на данном луче. Каждый отрезок О А изображает величину а, мера которой в единицах е равна к (рис. 3.11, где О, А = 2е).

Рис. 3.11. Кодирование величин отрезками.

Сложение чисел — мер величины. Так как две величины одного рода можно складывать и имеет место свойство аддитивности меры.

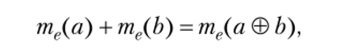
то сумма мер п = ттгДя) и к = т_в(Ь) равна.

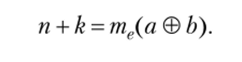
Согласно этому определению сумма п + к (п = 4, к = 2) в соответствии с принятым кодом представляется так, как на рис. 3.12.

Рис. 3.12. Представление суммы 4 + 2

Разность 6−2 находится рассуждением: число, которое надо прибавить к 2, чтобы получить 6, равно 4, так как 4 + 2 = 6. Из свойств сложения величин следуют коммутативность и ассоциативность сложения чисел — мер величины.

Умножение чисел — мер величины. Если 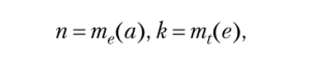то в силу свойства мультипликативности меры произведение.

На языке знаков-индексов произведение 2 • 3 в соответствии с данным определением находится так, как показано на рис. 3.13, где.

Рис. 3.13. Представление произведения 2 • 3

Это определение согласуется с определением умножения по Лобачевскому: каждая единица числа 3 замещается числом 2.

Отношение сравнения чисел — мер величины продуцируется соответствующим отношением величин, мерами которых эти числа являются, при условии что они измерены одной и той же единицей: если п = т_в(а), к = т_е(Ь), то п < k тогда и только тогда, когда а < Ь.

Отметим, что рассмотренные выше теоретические модели натуральных чисел являются результатом абстрагирования, обобщения и идеализации практических действий, продиктованных прежде всего жизненными потребностями человека. Именно поэтому эти модели занимают главенствующее место в обучении арифметике в начальной школе, тем не менее только ими не ограничивается и не может ограничиваться обучение младших школьников.

Задания для самостоятельной работы

• 1. Проанализируйте методику обучения сравнению величин по учебнику В. В. Давыдова с соавторами. Укажите этапы решения данной учебной задачи.
• 2. Постройте диалог, убеждающий в необходимости изобретения величины-посредника для сравнения величин. Воспользуйтесь заданиями учебника В. В. Давыдова с соавторами.
• 3. Укажите способы фиксации результата сравнения данной величины с величиной-посредником, предлагаемые в учебнике В. В. Давыдова. Объясните, почему каждый из этих способов есть обозначение числа — меры величины.
• 4. Составьте систему заданий, обучающих измерению величин, представленную в учебнике Г. В. Дорофеева и Т. Н. Мираковой.
• 5. Спроектируйте фрагмент урока на тему «Зависимость числового значения (меры) величины от выбранной единицы».
• 6. Составьте таблицу, используя учебники математики УМК «Школа России», «Перспектива, «Школа 2100».

• 7. Опишите методику обучения сложению чисел — мер величины. Воспользуйтесь учебником УМК «Перспектива».
• 8. Опишите методику обучения умножению чисел — мер величины. Воспользуйтесь учебником В. В. Давыдова с соавторами.
• 9. Меру величины называют также именованным числом. Раскройте особенности выполнения арифметических действий с результатами измерения времени как продолжительности того или иного процесса.
• 10. Опишите наглядные средства, необходимые для формирования умений производить арифметические действия с мерами массы.