Основные свойства преобразований Фурье

На практике важна связь между рядом преобразований сигнала и соответствующими этим преобразованиям изменениями его спектральной плотности.

1. Сложение, усиление и ослабление сигналов (теорема линейности).

К линейным операциям относят сложение, вычитание, усиление и ослабление сигналов, поэтому к ним применимо свойство линейности. Если имеется совокупность детерминированных сигналов u₂(t), …_; и0), …, u_s(t),

обладающих спектральными плотностями 5, (со), S₂(со), …, 5)(со), …, 5^со), то суммарному (разностному) значению сигналов.

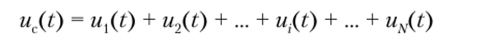
соответствует сумма (разность) их спектральных плотностей.

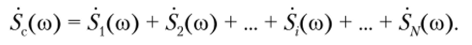
Данная теорема имеет элементарное доказательство: достаточно в прямое преобразование Фурье (2.29) подставить сумму исходных сигналов.

В общем виде теорему линейности записывают следующим образом:

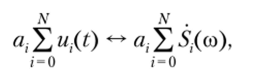
где a_i — произвольные числовые коэффициенты; i = 0, 1,…, N.

2. Сдвиг сигнала во времени (теорема запаздывания). Пусть сигнал u_x(t) со спектральной плотностью 5, (со) задержан на некоторое время t_c. В этом случае u₂(t) = u_x(t — t_c)> и спектральная плотность задержанного сигнала в соответствии с прямым преобразованием Фурье (2.29) имеет вид.

Введя новую переменную интегрирования т = t — t_c, получим.

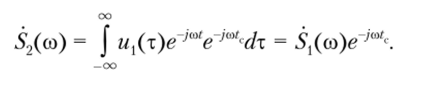
Итак, сдвиг исходного сигнала во времени на некоторый интервал t_c приводит к тому, что спектр задержанного сигнала оказывается равен спектральной плотности 5j (co), умноженной на комплексную экспоненту Амплитудный же спектр сигнала не меняется (ведь модуль такой комплексной экспоненты равен единице). При этом фазовый спектр приобретает дополнительное слагаемоесо?_с, линейно зависящее от частоты. На практике сдвиг исходного сигнала во времени осуществляют при аудиои видеозаписи. Теорема запаздывания показывает, что сколько бы долго ни хранилась такая запись, спектр (и форма) сигнала не претерпит изменений.

3. Смещение спектра сигнала (теорема смещения). Если S_{(со) — спектральная плотность сигнала u_{(t), то спектральная плотность S₂(со + Q), полученная путем сдвига исходного спектра, но оси частот на величину Q, соответствует сигналу u₂(t) = ^jQt. Действительно, согласно формуле (2.29).

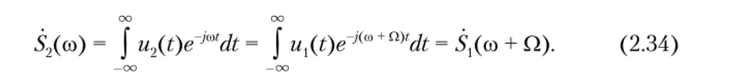
Это преобразование спектра импульсного сигнала применяют в системах связи либо при переносе спектра сигнала из одной полосы частот в другую, либо при модуляции. Формула (2.34) показывает, что в результате таких преобразований спектр сигнала смещается на величину Q, равную частоте сдвига.

4. Изменение масштаба времени. Пусть в исходном сигнале u_x(t) изменен масштаб времени так, что аргумент t умножен на постоянный коэффициент b и u₂(t) = u_x(bt). Если b > 1, то происходит «сжатие» исходного сигнала; если же 0 < b < 1, то исходный сигнал «растягивается» во времени. Докажем это.

Спектральная плотность измененного во времени сигнала.

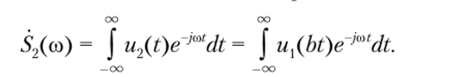
Введя новую переменную т = Ы, получим.

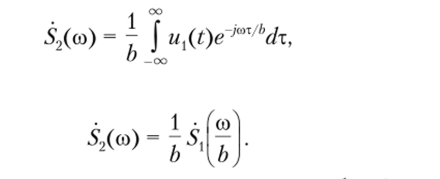
откуда Увеличение длительности импульсного сигнала любой формы в b раз сопровождается сжатием ширины его спектра во столько же раз, и наоборот, уменьшение длительности сигнала приводит к расширению его спектра.

5. Спектр произведения сигналов (теорема о свертке спектров). Прежде чем определить данный спектр, введем важное для теории сигналов понятие свертки двух функций. Рассмотрим скалярное произведение двух функций /(?) и h (t):

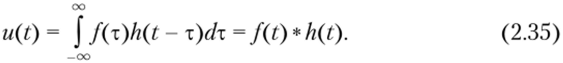
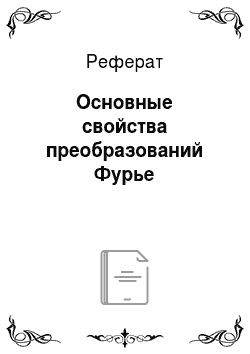
Это соотношение имеет фундаментальное значение в теории связи. Интеграл (2.35) в математике и теории цепей называют сверткой (англ, convolution) двух функций или сигналов (где * — знак операции свертки функций).

Пусть сигналы /(f) и h (t) имеют спектральные плотности /(со) и #(со) соответственно. Тогда их произведение u{t) = f{t)h{t) будет характеризовать спектральная плотность.

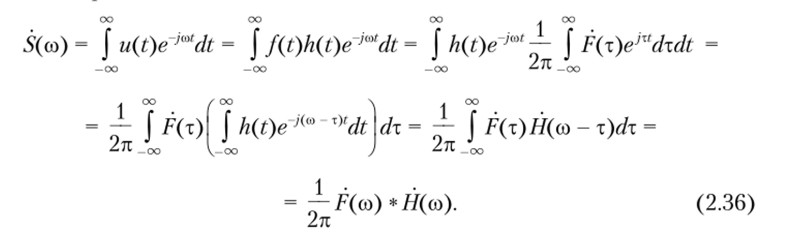
При выводе формулы (2.36) сигнал /(f) выражен через его спектральную плотность F (со) с заменой переменной со на т.

Согласно формуле (2.36) спектральная плотность произведения двух сигналов есть свертка их спектральных плотностей (умноженная на 1/(2л)), т. е. свертка, осуществленная ужй в частотной области. Данное соотношение имеет чрезвычайно важное значение в теории связи. Оно связывает спектральный и временной подходы к анализу импульсных сигналов и служит для целей исследования прохождения подобных сигналов через линейные и линейно-параметрические цепи.

Нетрудно убедиться, что операция свертки коммутативна, т. е. допускает изменение порядка следования преобразуемых функций: