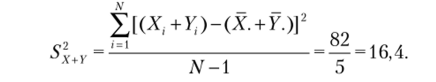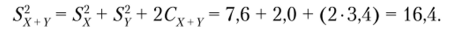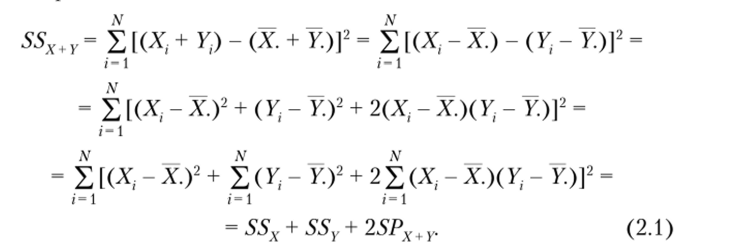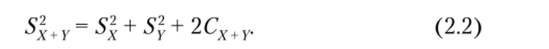Дисперсия суммы двух переменных
Отсюда следует важный вывод, что дисперсия суммы баллов, полученных из разных тестов, равна сумме дисперсий баллов исходных тестов только тогда, когда ковариация между исходными тестами равна нулю. Важным аспектом является соотношение между дисперсией суммы двух переменных и дисперсией переменных X и У. Вначале приведем само соотношение, а затем уже выведем его. Это соотношение имеет вид… Читать ещё >
Дисперсия суммы двух переменных (реферат, курсовая, диплом, контрольная)
Нередко мы заинтересованы в сложении результатов, полученных по двум разным тестам. Здесь важно понять, что при этом происходит с дисперсией. Мы рассмотрели это на примере наших тестов по арифметике (X) и алгебре (У) — Отметим, что среднее значение новой переменной (X + У) равно 8,0 (табл. 2.4).
Дисперсия переменной (X + У) равна.
Важным аспектом является соотношение между дисперсией суммы двух переменных и дисперсией переменных X и У. Вначале приведем само соотношение, а затем уже выведем его. Это соотношение имеет вид:
Результаты вычисления для переменной (X + У).
Таблица 2.4
Испытуемый. | X. | У | (Х+У,). | [(Х,+ У)-(Х + К)|. | 1(х, + у,) — (X. + К)]2 |
— 4. | |||||
— 5. | |||||
Сумма. |
Доказательство этого соотношения состоит в следующем. Рассмотрим сумму квадратов отклонений объединенной переменной от ее среднего значения.
Последний член выражения SPX+Y представляет собой сумму произведений отклонений значений переменных X и Y от их средних значений. Если каждое слагаемое разделить на N — 1, то мы получим дисперсии из сумм квадратов и ковариацию из суммы произведений:
Отсюда следует важный вывод, что дисперсия суммы баллов, полученных из разных тестов, равна сумме дисперсий баллов исходных тестов только тогда, когда ковариация между исходными тестами равна нулю.