Регрессия и корреляция тестовых баллов

Предсказание, или прогноз, является одной из важных функций науки. Например, в области образования часто необходимо сделать прогноз по успеваемости школьников по одному учебному предмету на основе успеваемости по другому учебному предмету. После окончания обучения мы можем сравнить полученные результаты с прогнозом и таким образом определить точность прогноза.

Самой простой моделью, которую можно использовать для прогноза, является линейная регрессионная модель.

Линейная регрессионная модель

В качестве модельного примера рассмотрим данные тестирования шести школьников по арифметике и алгебре. Определим, можно ли на основе успеваемости школьников по арифметике предсказать успеваемость этих школьников по алгебре.

На первый взгляд может показаться, что речь идет о детерминистской модели, такой как в физике. Например, закон Ньютона констатирует, что если к телу массой т приложить силу F, то тело будет двигаться с ускорением а. Все эти переменные связаны соотношением F = та. Это строго детерминированная зависимость.

Для получения прогноза мы будем использовать уравнение такого же вида:

Однако трудность использования этого уравнения состоит в том, что оно предполагает, что для конкретного значения X мы можем точно предсказать значение Y. На рис. 2.1 видно, что это сделать невозможно.

Рис. 2.1. Величина тестового балла по алгебре в зависимости от тестового балла по арифметике

Если бы уравнение (2.3) было применимо, то можно было бы провести прямую линию, на которой лежали бы все точки. Лучшее, что мы можем сделать, — это провести прямую, которая была бы как можно ближе ко всем точкам, и затем использовать эту прямую для получения прогноза. Таким образом, для г-го школьника с тестовым баллом X_i (например, для школьника 4 тестовый балл равен 10) мы можем предсказать тестовый балл по алгебре, используя уравнение (2.4):

Отметим, что для школьника под номером 4, у которого тестовый балл по арифметике равен 10, прогноз тестового балла по алгебре равен 3,79, хотя на самом деле его тестовый балл по алгебре равен 4. Так что в этом случае ошибка прогноза равна 0,21 балла. В общем виде это можно выразить следующим образом:

Для школьника 4 уравнение (2.5) приобретает вид:

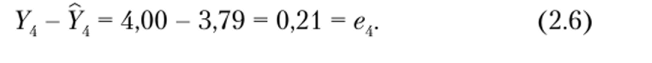
11еобходимо подчеркнуть, что в этом виде прогноза мы допускаем ошибку прогноза. Чтобы подчеркнуть это, запишем модель (2.3) не в виде детерминистической модели, а в виде вероятностной модели, которая допускает ошибку прогноза:

Коэффициенты р₀ и Р, должны быть такими, чтобы минимизировать сумму квадратов ошибок, т. е.

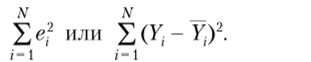
Необходимо подчеркнуть, что коэффициенты р_ц и р, используются в случае рассмотрения всей совокупности школьников, из которых извлечена наша выборка в шесть школьников. Чтобы подчеркнуть, что мы работаем с выборкой, а не со всей популяцией, будем использовать для обозначения коэффициентов вместо греческих букв Р₀ и р, которые используются для обозначения истинных параметров (для всей популяции), латинские буквы Ь₀ и 6, (для выборки из совокупности).

Оценки, полученные с помощью метода наименьших квадратов, имеют вид Для нашей выборки оценки параметров равны.

Если мы проведем линию Y = -0,682 + 0,447Х, то получится график, изображенный на рис. 2.2.

Рис. 2.2. Уравнение регрессии для прогноза тестового балла по алгебре на основе тестового балла по арифметике.

Ошибки прогноза можно определить непосредственно из графика или точно вычислить на основе уравнения:

Все вычисленные ошибки приведены в табл. 2.5.

Таблица 2.5

Ошибки прогноза.

Ошибки прогноза Y_j-Y_i в этой таблице соответствуют пунктирным отрезкам на графике, которые показывают расхождение между прогнозом и тестовым баллом по алгебре. Например, для тестового балла по арифметике, равного 7, прогнозируется, что тестовый балл по алгебре равен 2,45. На самом деле один школьник с тестовым баллом по арифметике, равным 7, получил по алгебре тестовый балл, равный 3. Таким образом, тестовый балл по алгебре недооценен, ошибка прогноза равна 0,55. Другой же школьник с тестовым баллом 7 по арифметике получил 2 балла по алгебре, так что здесь тестовый балл переоценен, ошибка прогноза равна -0,45.