Устройство и принцип действия многофазных электрических машин

Началом истории многофазных электрических машин принято считать 1887 г., когда Н. Тесла запатентовал двигатель, который по нынешней терминологии представляет асинхронный двигатель. Основанный на образовании бегущего магнитного по. ля многофазной системой переменных токов, созданный двигатель обладал высокими эксплуатационными показателями и, что очень важно, развивал необходимый пусковой момент, превосходя при этом своей простотой и надежностью коллекторный двигатель постоянного тока. В дальнейшем было доказано преимущество многофазной (трехфазной) системы для создания генераторов, трансформаторов и линий электропередач, которая в конечном счете вытеснила постоянный ток Применение последнего сохранилось в специальных областях. Заметим, что в настоящее время 95% мощности в современных электроприводах реализуется асинхронными двигателями; это составляет примерно половину вырабатываемой электрической мощности, которая создается многофазными генераторами.

Рассматривая современное состояние электротехнической промышленности, можно сказать, что изобретение многофазной системы токов для создания бегущего магнитного по. ля является наиболее удачным практическим воплощением закона электромагнитной индукции, открытого М. Фарадеем.

Рассмотрим образование бегущего магнитного поля на примере простейшей. двухполюсной трехфазной машины, приведенной на рис. 3.8. Здесь каждая фаза А-х> В-у, C-z изображена в виде катушки, соста&тенной из витков с диаметральным шагом. Их плоскости смещены относительно друг друга на угод 120°. За положительное наираатешю тока в фазах примем такое, когда в начале фаз А, В, С они входят в плоскость рисунка. Оси магнитных полей, которые лежат на перпендикулярах к сере, дине плоскостей катушек, также будут сдвинуты на 120°, если за положительное напраатешю оси принять направление магнитного потока, созданного положительным током.

Рис. 3.8. Простейшая трехфазиая обмотка статора и создаваемое магнитное поле при протекании симметричной трехфазной системы токов.

в моменты времени:

a-f = 0; б-f = со, /= 120°; в — f = о, t = 240°.

Д алее примем, что магнитное поле, создаваемое током фазы, представляет синусоидальную пространственную волну, которая обеспечивается мероприятиями, связанными с распределением проводников (витков) вдоль поверхности статора, как это будет показано ниже. Только выполнение указанного требования обеспечивает неизменную форму бегущего результирующего поля.

Найдем результирующее магнитное поле, созданное трехфазной синусоидальной системой токов:

Полагая, что индукция магнитного поля пропорциональна величине протекающего тока /" (п = А, В, С), на рис. 3.8 (в последовательности а-б-в-а) показан характер изменения магнитных полей отдельных фаз и создаваемое ими результирующее магнитное поле за полный период изменения тока фазы А.

Магнитные поля отдельных фаз представляют синусоидальные волны, пульсирующие с частотой протекающего тока. Они могут быть представлены векторами В_А, В_в, В_с, по абсолютной величине равными амплитуде волны и направленными вдоль нее, т. е. для выбранной системы координат эти векторы лежат на осях фаз. Результирующее поле, представляющее сумму синусоидальных полей отдельных фаз, будет также представлять синусоидальную волну, бегущую в пространстве относительно обмоток статора с угловой скоростью coi = 2я/|, проходя за период изменения тока фазы путь, равный двойному полюсному делению 2 т, которому в общем случае соответствует угол 2я электрических радиан.

Очевидно, что результирующее поле В, найдется как сумма векторов В," характеризующих пульсирующие поля отдельных фаз. Дтя этого упорядочим систему координат, использованную при построениях на рис. 3.8. С этой целью проведем шюскость, перпендикулярную оси вращения, и примем точку пересечения за начало прямоугольной системы координат, вещественную ось которой совместим с осью фазы А, как показано на рис. 3.9, б.

Вектор индукции результирующего поля В., найдется как сумма векторов индукции отдельных фаз В":

которые показаны на рис. 3.8 (в последовательности абва), откуда видно, что они представляют пульсирующие с частотой тока векторы, лежащие на осях фаз, сдвинутых в пространстве на угол 120°. Их абсолютное значение пропорционально протекающим токам i".

где Л — коэффициент пропорциональности.

Тогда с учетом (3.3) и того обстоятельства, что ось фазы Л совмещена с осью вещественных чисел, получим выражение для вектора результирующего поля (3.2):

где a =e^jl20 и a² =e^jl20 представляют операторы поворота, приводящие мгновенные значения фазных токов /," откладываемых на оси вещественных чисел (с ней совмещена ось времени) к направлениям магнитных потоков, создаваемых ими, как показано на рис. 3.9, б.

Рис. 3.9. Построение результирующих) вектора индукции при Л = 1:

а — ipoika векторов, представляющих фазные токи; б — приведение токов к пространственным осям обмоток Для случая, когда токи фаз представляют симметричную систему токов (3.1), после подстановки их в (3.4) получим.

откуда видно, что результирующее поле, представленное вектором В_у, имеет амплитуду в 3/2 раза большую амплитуды пульсирующего поля и вращдется в пространстве с угловой скоростью сщ. Этот же результат можно было бы наблюдать из последовательности изменения магнитных полей за полный период изменения тока, как показано на рис. 3.8.

Бегущее магнитное поле может быть создано и двухфазной системой токов, в которой между протекающими токами угол сдвига составляет 90°:

и на такой же угол сдвинуты в пространстве оси фаз, тогда вектор результирующего поля В_Л по аналогии с предыдущим случаем найдется из следующего выражения:

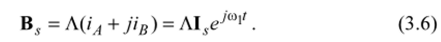
Здесь оператор поворота равен j = e^Jn>2.

Полученное выражение для В_Л показывает, что создаваемое двухфазной системой магнитное поле представляет бегущую в пространстве волну, аналогичную создаваемой трехфазной системе токов.

Аналогию между бегущими полями, создаваемыми двухфазной и трехфазной системами токов, легко обнаружить из выражения для B. v (3.5), если представить экспоненциальную функцию в соответствии с формулой Эйлера.

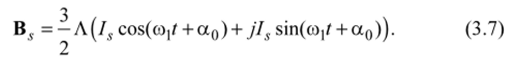
Полученное выражение показывает возможность представления трехфазной системы токов эквивалентной ей двухфазной. Сдеданное замечание относится к любой многофазной системе. Оно исходит из того, что для определения положения векторов на плоскости достаточно двух координат.

На принципе бегущего магнитного поля созданы следующие типы электрических машин:

• 1) асинхронные машины;
• 2) синхронные машины;
• 3) машины двойного питания.
• 1. Устройство и принцип действия асинхронной. машины

В пазах сердечников статора и ротора, выполненных на поверхностях, обращенных к воздушному зазору, размешаются многофазные.

Рис. 3.10. Взаимное положение контуров токов статора и ротора.

обмотки. При протекании в обмотках статора многофазной системы переменных токов с частотой / образуется бегущее магнитное поле, которое индуцирует ЭДС в обмотках ротора, и если она замкнута, то в ней начнут протекать токи, частота которых fi при неподвижном роторе равна частоте сети /. Создаваемое результирующее поле от токов ротора будет вращаться в пространстве со скоростью о)2, равной скорости бегущего поля статора со_ь т. е. они неподвижны относительно друг друга. Если активное сопротивление контуров ротора нс равно нулю, то между осями магнитных полей будет угол, меньший я радиан (рис. 3.10). В результате возникнет вращающий момент, стремящийся совместить оси эквивалентных контуров токов статора и ротора.

Под действием возникшего момента ротор начнет движение за бегущим полем статора, при этом изменится частота токов /2, она будет определяться разностью скоростей бегущего поля coi и скорости ротора со:

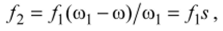
где величина скольжения s представляет разность скоростей, измеренную в долях от скорости соь называемой синхронной скоростью.

В новых условиях пространственная скорость бегущего поля складывается из скорости поля ротора со₂ = 2л/₂ относительно ротора и скорости самого ротора со: со + со₂.

Если выразить эти скорости через скольжение .9 и синхронную скорость со, найдем, что.

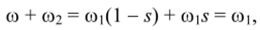
т. е. и в новых условиях пространственная скорость полей от токов статора и токов ротора оказывается одинаковой, следовательно, как и при неподвижном роторе, эквивалентные контуры токов будут стремиться занять соосное положение, т. е. ротор будет бежать за бегущим полем статора. Такая картина будет наблюдаться до тех пор, пока скорость ротора не достигнет синхронной скорости соь В этом случае наводимая ЭДС в обмотке ротора будет равна нулю, соответственно, будут равны нулю ток и развиваемый момент. Если далее за счет внешнего момента скорость ротора увеличить, то возникшие токи создадут электромагнитный момент, действующий встречно внешнему, в этом случае последний преодолевает стремление контуров занять соосное положение. Рассмотренный режим работы, когда со > со i, является генераторным режимом.

Асинхронные двигатели, таким образом, развивают вращающий момент при любой скорости вращения ротора, как и двигатели постоянного тока развивают пусковой момент, т. е. обладают важнейшим эксплуатационным показателем, который наряду с простой и дешевой конструкцией обеспечил массовое применение асинхронным двигателям. Можно утверждать, что изобретение асинхронного. двигателя создало основу широкого применения элекгонриводов в народном хозяйстве.

2. Синхронные машины имеют на статоре такую же многофазную обмотку, как в асинхронной машине. На роторе располагается обмотка возбуждения, по которой протекает постоянный ток (fi = 0). Поэтому здесь скорость поля ротора равна механической скорости ротора и, следовательно, только при скорости ротора, равной скорости бегущего поля статора соь эквивалентный контур токов статора и контур токов ротора будут взаимно неподвижны, только на этой скорости будет создаваться вращаюшдй момент, обусловленный стремлением контуров токов занять соосное положение. Название «синхронные машины» и обусловлено именно тем, что они развивают момент при скорости ротора, равной скорости поля оз], которую называют синхронной скоростью. На рис. 3.11 представлены конструкции синхронных машин, отличающихся исполнением обмотки ротора.

Рис. 3.11. Устройство явнопошосной (а) и неявнополюсной (6) синхронной машины:

1 — статор (якорь); 2 — ротор (индуктор); 3 — обмотка возбуждения Так называемая явнополюсная конструкция ротора используется при создании синхронных машин на скорости вращения п < 1500 об/мин. Для скоростей п > 3000 об/мин ротор выполняется неявнополюсным. Такое различие в конструкции роторов связано с обеспечением механической прочности. Синхронные машины в основном используются в качестве источников электрической энергии — генераторов. Они, в отличие от асинхронных генераторов, могут вырабатывать наряду с активной мощностью и реактивную, необходимую для работы трансформатров и асинхронных машин.

В настоящее время в связи с появлением магнитных сплавов с высокими значениями энергии все шире создаются синхронные двигатели с возбуждением от постоянных магнитов мощностью от долей ватта до нескольких сотен киловатт.

3. Машины. двойного питания. В рассматриваемом виде машин на статоре и роторе располагаются многофазные обмотки, которые подключены к многофазным источникам питания, имеющим в общем случае различные частоты f и fi- Принцип действия, как и в ранее рассмотренных машинах, основан на взаимодействии контуров токов статора и ротора через создаваемые ими бегущие поля. Скорость ротора будет определяться алгебраической разностью частот, причем частоты считаются положительными при одинаковом чередовании фаз на статоре и роторе.