Продуктивные матри11ы и их свойства

В экономике особенно широко применим класс неотрицательных матриц, у которых все элементы являются неотрицательными. Для них справедлива следующая важная теорема (приводится без доказательства).

Теорема 3.4 (теорема Фробениуса — Перрона). Для любой неотрицательной матрицы А существует собственное значение Х_Л > 0 (число Фробениуса), такое, что все другие собственные числа X этой матрицы удовлетворяют неравенству Х_А? |Х|, причем существует соответствующий собственный вектор х_А (вектор Фробениуса), который является неотрицательным. Если же матрица А положительная, то Х_л > 0 и вектор х_А также является положительным. ?

Рассмотрим матричное уравнение.

где А — неотрицательная квадратная матрица порядка п, X и У — векторыстолбцы или, что-то же самое, матрицы размера их 1. Уравнение (3.26) будет использовано в последующих разделах; оно играет чрезвычайно важную роль в балансовых моделях экономики.

Определение 6. Неотрицательная матрица А называется продуктивной, если для любого неотрицательного вектора У порядка п существует неотрицательный вектор X того же порядка.

Группируя члены, содержащие вектор Л', в правой части, получаем уравнение:

Если матрица А является продуктивной, то матрица (?- А) должна быть невырожденной, так как выражение для X получается умножением слева обеих частей матричного уравнения (3.27) на матрицу (? — Л)'¹

Для уравнения типа (3.26) разработана соответствующая математическая теория исследования решения и его особенностей. Укажем некоторые се основные моменты. Приведем без доказательства важную теорему, позволяющую устанавливать продуктивность матрицы А.

Теорема 3.5. Если для матрицы А с неотрицательными элементами и некоторого вектора у с неотрицательными компонентами уравнение (3.26) имеет решение х с неотрицательными компонентами, то матрица А продуктивна. ?

Иными словами, достаточно установить наличие положительного решения системы (3.26) хотя бы для одного положительного вектора у, чтобы матрица А была продуктивной.

Для определения продуктивности неотрицательных матриц существует несколько взаимосвязанных критериев. Приведем их.

Матрица А продуктивна, если она удовлетворяет одному из критериев.

1. Максимум сумм элементов в ее столбцах не превосходит единицы:

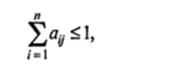
причем хотя бы одна сумма строго меньше единицы.

• 2. Матрица (? — А) невырождена, и матрица (? — А)~^[ неотрицательна.
• 3. Число Фробениуса для матрицы А меньше единицы: Х_л < I.

Определение 7. Запасом продуктивности матрицы А называется такое число, а > 0, что при 1 < X < 1 + а матрица ХА продуктивна, а матрица (1 + а)А не является продуктивной.

Величина запаса продуктивности характеризует сохранение продуктивности матрицы А при увеличении компонент вектора Y.

Пример 11. Найти запас продуктивности матрицы.

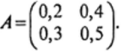
Нетрудно убедиться, что данная матрица А является продуктивной. Матрица (? — ХА) имеет вид:

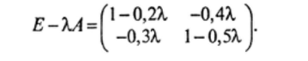
Определитель этой матрицы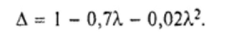

Согласно второму критерию продуктивности матрица (Е — АЛ) должна быть невырожденной, а все элементы ее обратной матрицы.

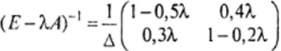
должны быть неотрицательными. Эти условия выполняются, если, А > 0 и X < 2.

Решением соответствующего квадратного неравенства является интервал Хе (-36,375; 1,375). Из второго условия и того, что X > 0, получаем X < 1,37. Однако согласно первому критерию продуктивности имеем X < 1,11. Выбирая минимальное значение, получаем запас продуктивности, а * 0,11.

Приведем без доказательства одну важную теорему из теории матриц, которая понадобится нам далее.

Теорема 3.6. Если бесконечный ряд, составленный из степеней квадратной матрицы Л, сходится, то его сумма есть матрица (? — Л)^-1

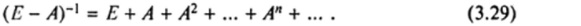
Четвертым критерием продуктивности неотрицательной матрицы можно считать выполнение теоремы 3.6. Аналогом разложения (3.29) является сумма членов бесконечной геометрической прогрессии с первым членом, равным единице и положительным знаменателем q < 1.

В этой части мы будем далее рассматривать упражнения с продуктивными матрицами (глава 5).