Контрольные задания и задачи для самостоятельного решения

Задачи на вычисление определенных интегралов без использования замены переменной и интегрирования по частям.

3.1. Используя геометрический смысл определенного интеграла как площади криволинейной трапеции и изобразив эскизы графиков подынтегральных функций, вычислите (квадратные скобки ниже означают целую часть числа: [х] — наибольшее целое число, не превосходящее х; фигурные скобки — дробную часть: {х} = х- [х]):

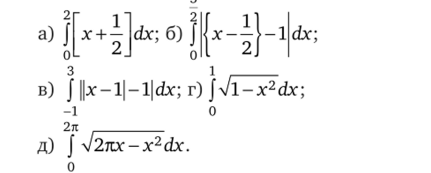
3.2. Вычислите интегралы:

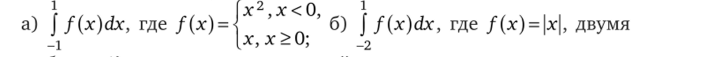
способами: 1) вначале используя свойство аддитивности интеграла; 2) сразу с помощью формулы Ньютона — Лейбница.

3.3. Найдите интегралы:

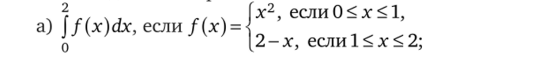
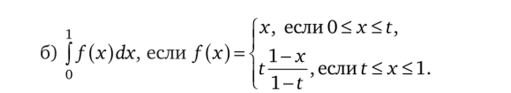
3.4. Найдите ошибку в рассуждениях при вычислении следующих интегралов:

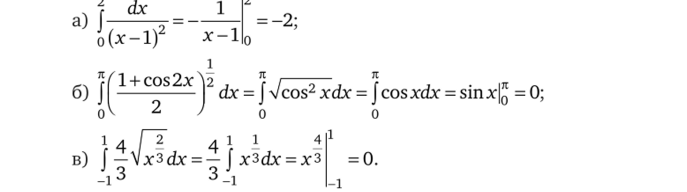
3.5. Вычислите определенный интеграл от ограниченной разрывной функции, разбивая промежуток интегрирования на части так, чтобы на каждой из них однозначно раскрывалась целая часть (используя.

свойство аддитивности): j[e^x]dx.

о.

R f RwruT/frггтлгтр ннтргпя ттта пт огпя штл tjpt-t т-ттл y пяяпкттттчту гЬл/итплй*.

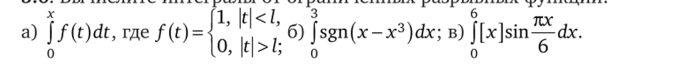
3.7. Вычислите интегралы от ограниченных разрывных функций: 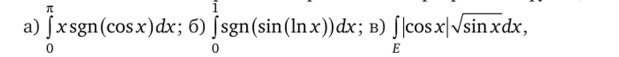где Е — множество тех значений отрезка [0,4л], для которых подынте;

тральное выражение имеет смысл.

sh2 fa

3.8. Вычислите интеграл J ,.

shlVl + X²

3.9. Пусть дифференцируемая на отрезке [0,3] функция y-f (x) в точках х -1 и х — 3 имеет локальные минимумы y_min = 2 и y_min = 0.

соответственно, а в точках х = 0 и х = 2 — локальный максимум у_тах = 4. з Вычислите J|/'(x)|dx. о Замена переменной при вычислении интегралов.

• 3.10. Найдите ошибки в рассуждениях:
• 2л dx
• а) | ——г——. Применяя подстановку t = tgx, получаем

о (2 + tg²x)cos²x.

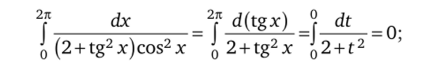aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">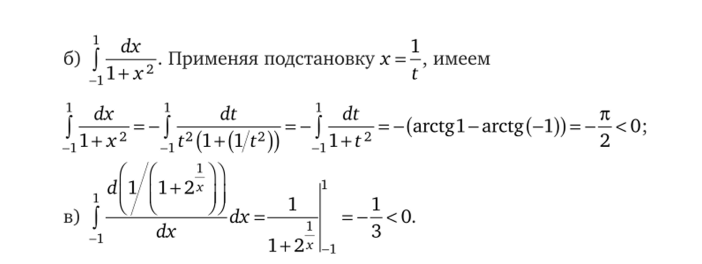

3.11. Можно ли вычислить интеграл jJl-x²dx с помощью замены о.

переменной x = sinf, взяв в качестве новых нижнего и верхнего пределов интегрирования числа П, 1₂: а) я и л/2; б) 2л; и 5л/2; в) л и 5л/2? Вычислите интеграл в каждом случае, когда указанная замена допустима.

3.12. Применимы ли указанные подстановки в следующих интегралах (в каждом случае приведите обоснование, почему):

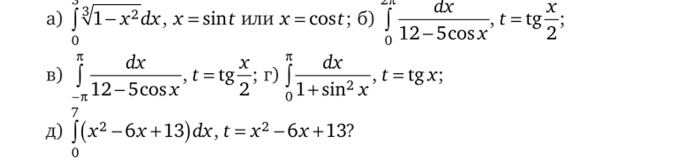
3.17. Пусть функция / непрерывна на отрезке [а, Ь], причем f (a + b-x) = f (x) для любых х е [а, Ь]. Докажите, что.

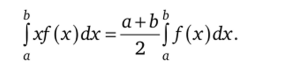
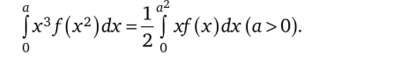
3.19. Докажите равенство.

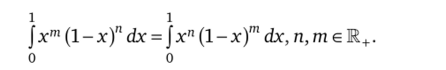
3.20. Пусть/— непрерывная функция на отрезке [А, B]z>[a, b], Най- d ^ь

дите —[f (x + y) dy при А-а<�х<�В-Ъ. dx^J_a

^ 9 1 R^TUT^r ТТТЛТ?" ТуТМ’Г^Г'ПР П1чТ*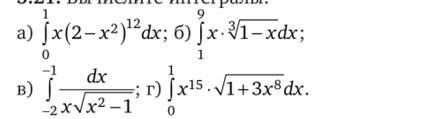

3.22. Применяя подходящую замену переменной, вычислите инте^[1]

гралы:

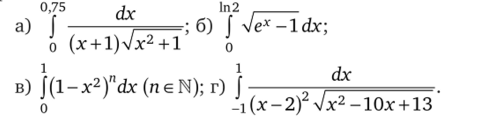
9 9R RtauLrr тттлтр мптргпя тттл*.

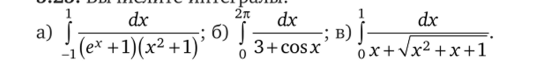
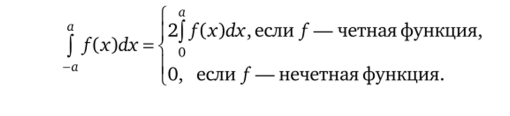
3.28. Вычислите интегралы, полагая t-x—:

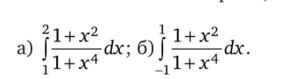х.

3.29. Вычислите с помощью тригонометрических подстановок интегралы:

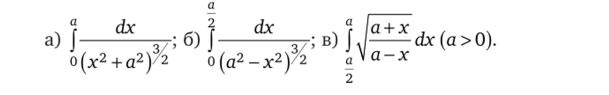
Интегрирование по частям.

3.30. Применяя формулу интегрирования по частям, найдите.

J |1пх|сЬс.

%.

3.31. Интегрируя по частям, вычислите интегралы:

п е

a) Je* cos² xdx; б) J (xlnx)²dx о 1.

• 1 ^ х&^ dx 2
• 3.32. Докажите неравенство —< [. ==<�—j=.
• 5 ³₀sl25-x + x² ЗТИ
• 3.33. Пусть / > 0, /' < 0 на отрезке [0,1]. Докажите, что

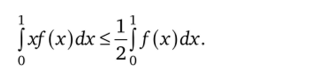
• 3.34. Вычислите пределы последовательностей:
• 1 л к

a) lim Jcos (x'^!)dx; б) lim Jcos (x:'^l)dx; в) lim Jcos (x'')dx:.

П—>+°° q П—>4-oo ^ П—>4-oo q.

Можно ли при вычислении данных пределов использовать первую теорему о среднем?

3.35. Пусть/— непрерывно дифференцируемая на отрезке [а,?>] функция. Вычислите пределы последовательностей: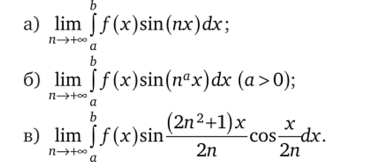

3.36. Выведите формулу понижения по параметру п и с ее помощью 1.

вычислите интеграл I_n = Jх^т (1пх)" dx (т, п е N). о.

Jt/2.

3.37. Вычислите интеграл J sin^2m xcos²" xdx (n, meN) с помощью о.

формулы понижения по одному из параметров.

3.38. Вычислите интегралы: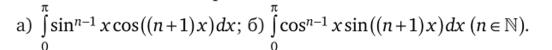

к/2

3.39. Вычислите интеграл J cos 2пх In cos xdx (пе N).

о Интегрирование периодических функций.

3.40. Докажите, что если периодическая с периодом Т функция/ интегрируема на каждом конечном отрезке, то для любых а, ЬеШ

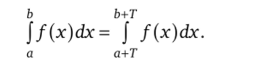
3.41. Пусть непрерывная на всей числовой прямой функция/является периодической с периодом Г. Докажите, что первообразная F

функции/является периодической (с тем же периодом) тогда и только т

тогда, когда J f (t)dt = 0. о.

3.42. Докажите, что если / — непрерывная периодическая функция, определенная при -°°<�х и имеющая период Тф0, то.

а+Т т

J /(x)dx = J/(x)dx для любого действительного а.

а 0.

3.43. Докажите, что если для непрерывной на (-оо, + оо) функции/.

х+1.

для любого х выполняется равенство J f (t)dt = 0, то/ периодическая.

х;

Найдите период этой функции.

3.44. Пусть непрерывная на всей числовой прямой функция / явля;

ется периодической с периодом Г. Докажите, что функция F (х) = J/(t)dt.

о является суммой периодической функции с периодом Т и линейной А ^т

функции —х, где А = j f (t)dt.

Т о.

• 2 л dx
• 3.45. Найдите интеграл j ——-—.

q sin⁴x + cos⁴x.

3.46. Докажите, что если функция /еС[0,1], то верно соотношение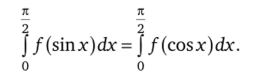

Интегрирование функций, имеющих оси и центры симметрий.

3.47. Докажите, используя геометрический смысл интеграла, что если функция / непрерывна на отрезке [-а, а], симметричном относительно х = 0, то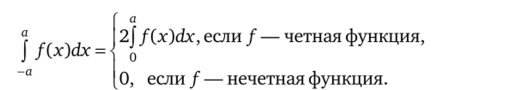

• 3.48. Докажите, что одна из первообразных четной непрерывной функции есть функция нечетная, а всякая первообразная нечетной непрерывной функции есть функция четная.
• 3.49. Вычислите определенные интегралы:

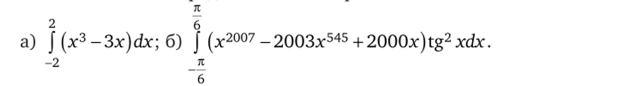
• 2л
• 3.50. Докажите, что J sin (sinx + nx) dx = 0(neN).

о.

3.51. О непрерывной функции / известно, что она нечетная на от;

X

резке [-Г/2, Т/2] и имеет период, равный Т. Докажите, что J f (t)dt есть о.

также периодическая функция с тем же периодом.

Интегрирование взаимно обратных функций 3.52. Докажите, что если функция/дифференцируема и обратима на отрезке [a, b], g — обратная для/функция, определенная на /([а, Ь]), то функция.

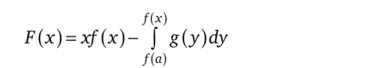
является первообразной для функции/на [а, Ь].

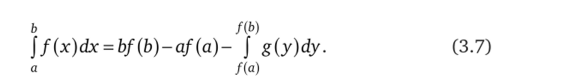
Используя полученный результат, докажите справедливость равенства.

• 1
• 3.53. Вычислите интеграл Jarctgxdr двумя способами: 1) используя

о формулу интегрирования по частям; 2) сведением к соответствующему определенному интегралу от функции, являющейся обратной к подынтегральной (по формуле (3.7) из предыдущей задачи).

юо.

• 3.54. Следующие интегралы вычислите двумя способами:
• 1) используя результат задачи 3.52;
• 2) пользуясь геометрическим смыслом определенного интеграла:

е²

б) j In xdx; в) О е

a) Jarcsinxdx;

dx.

1 + Vx.

Интегрирование гиперболических функций.

3.55. Вычислите интегралы:

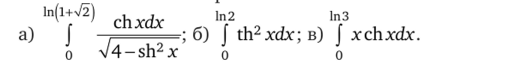aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">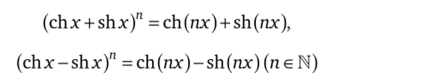

3.56. Докажите формулы понижения степени (их следствиями будут формулы.

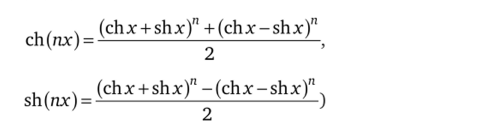
и с их помощью вычислите интегралы:

ОД 1п2 ОД 1п2.

a) J (chx + shx)¹⁰dx; б) J (chx-shx)¹⁰dx. о о.

• (_ех__е-х^п (е^х+е~^х)^п
• 3.57. Используя соотношения sh'^!x = —— и ch^x^-⁵¹——,
• 2^п 2^п

докажите формулы понижения степени.

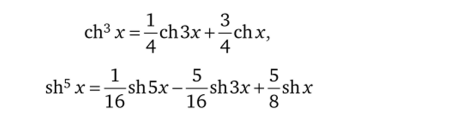
I¹" ²

и с их помощью вычислите интегралы: a) J ch³ xdx; б) Jsh⁵ xdx.

о о.

3.RR. Вычиглитр интргпялы^-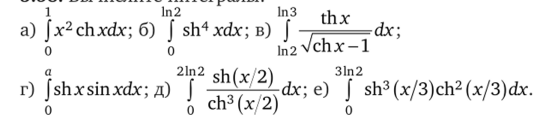

• [1] fa 3.24. Вычислите интеграл Г —-(0 < а < л). _а x2−2xcosa + l 3.25. Найдите положительную дифференцируемую на [0, + °о)функцию/, если известно, что при замене независимой переменной X t, = J f{t)dt она переходит в функцию е~*=.о ?JlK 3.26. Докажите, что J sin (x2)dx>0. о 3.27. Докажите, используя замену переменной интегрирования, чтоесли функция/непрерывна на отрезке [-а, а], симметричном относительно х = 0, то