Критерий Коши сходимости (расходимости) несобственного интеграла

Пусть функция / определена на промежутке [а, + °°) и интегрируема в собственном смысле на любом отрезке [a, A] (VA > а).

Теорема 4.1 (критерий Коши сходимости интегралов 1-го рода).

+оо.

Для сходимости интеграла J f (x)dx необходимо и достаточно, чтобы

а

для любого (сколь угодно малого) положительного числа е нашлось такое отвечающее ему число Д - Д (е) > а, что при любых А', А" > Д справедливо неравенство

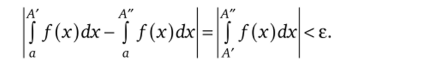
л.

Доказательство. Пусть F (A) = J/(x)dx. Тогда по критерию Коши.

а

существования предела функции в точке функция F имеет предел в точке +°° тогда и только тогда, когда для любого е>0 найдется число Д=Д (е)>а, такое что для любых А', А" >Д выполнено |F (A') — F (A")| < ?. Теорема доказана.

Как следствие, получаем следующую теорему.

Теорема 4.2 (критерий Коши расходимости интегралов 1-го.

+оо рода). Интеграл J f (x)dx расходится тогда и только тогда, когда

а

существует е > О, такое что для любого (сколь угодно большого) числа Aq > а найдутся такие два числа А', А" > Д, для которых выполняется неравенство

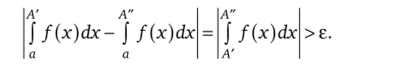
Пусть функция / определена на промежутке [а, Ъ] за исключением, быть может, точки Ъ, и интегрируема в собственном смысле на любом отрезке [а, Ъ — е], 0 < е < Ъ — а.

Теорема 4.3 (критерий Коши сходимости интегралов 2-го рода).

ь

Для сходимости несобственного интеграла j f (x)dx ф — особая точка).

а

необходимо и достаточно, чтобы для любого е > 0 существовало такое отвечающее ему число 5(e) >0, что при любых ц', х", таких что 0< Г|' < 5 и 0 < г)" < 5, выполнялось неравенство

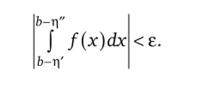
пз n.

Доказательство. Пусть F® = jf (x)dx. Тогда по критерию Коши.

а

существования предела функции в точке функция F имеет предел в точке b слева тогда и только тогда, когда для любого е > 0 найдется число 6(e)> 0, такое что для любых Г|', Г|", удовлетворяющих неравенствам 0 < ц' < 6 и 0 < Г|" < 6, выполнялось F (br')-F (b- r|")| < е. Теорема доказана.

Из данной теоремы вытекает следующее утверждение.

Теорема 4.4 (критерий Коши расходимости интегралов 2-го ро;

ь

да). Интеграл J/(x)dx (Ь — особая точка) расходится тогда и только

а

тогда, когда найдется е > 0, такое что для любого (сколь угодно малого) 6 > 0 найдутся числа т|', Г|", удовлетворяющие неравенствам 0 < ц' < 8, О < ц" < 8 и такие, что выполняется неравенство

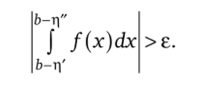
Пример 4.5.

Используя критерий Коши расходимости несобственных интегралов, дока;

Sin X

зать расходимость интегралов f-dx и f-dx (a>, p<0).

а ^хР а ^хР

+оо.

Решение. Согласно критерию Коши интеграл J f (x)dx расходится тогда.

а

и только тогда, когда.

В рассматриваемом случае интеграл расходится ф=> Зе > 0: VA > а ЗА', А" > А:

А"

^л sin X

-dx >е. Покажем, что это так. Действительно, так как VA >а Зп е N:

а- ^хР

2кп> А, то возьмем в качестве А' и А" числа 2кп и к + 2т соответственно и рассмотрим интеграл.

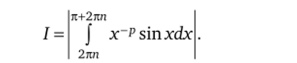
Функция дгр непрерывна на отрезке [2кп, к + 2тот], а функция sin х непрерывна и не меняет своего знака на этом отрезке, поэтому по первой теореме о среднем (теорема 2.1) имеем.

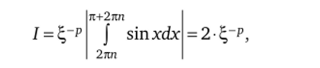
где 2пп < 4 < к + 2пп.

При достаточно больших пимеем-р>0,%>1, поэтому ZyP > 1 и, значит, I > 2. Но тогда для любого положительного е < 2 выполнен критерий Коши расходимости интеграла —dx. Таким образом, расходимость интеграла дока;

; хр Расходимость интеграла J —— dx доказывается аналогично.