Вопросы и задания для повторения

• 1. Дать определение функции распределения и плотности распределения непрерывной случайной величины.
• 2. Сформулировать и доказать свойства плотности распределения.
• 3. Как найти вероятность попадания случайной величины на промежуток (х,; х₂) по графику плотности распределения?
• 4. Дать определение математического ожидания и дисперсии непрерывной случайной величины.
• 5. Дать определения начального и центрального моментов, коэффициентов асимметрии и эксцесса.
• 6. Сформулировать понятие равномерного распределения, плотность и ее график, функция распределения, математическое ожидание, дисперсия, мода.
• 7. Сформулировать понятие показательного распределения, указать его параметры.
• 8. Сформулировать понятие распределения Лапласа, указать его параметры.
• 9. Сформулировать понятие нормального распределения, указать его параметры.
• 10. Что такое стандартное нормальное распределение?
• 11. Как вычислить вероятность попадания нормально распределенной случайной величины на отрезок [х_х; х₂]?
• 12. Что такое точность измерения?
• 13. Если случайная величина t, распределена нормально, Ъ, ~ N (a, о²), как

распределена случайная величина ц = + Р?

• 14. Как распределена сумма нормально распределенных случайных величин?
• 15. Вывести формулу для центральных моментов нормально распределенной случайной величины.
• 16. Сформулировать понятие логнормального распределения, указать его параметры.

Примеры решения задач

Задача 6.1. Плотность распределения случайной величины Ъ, имеет вид.

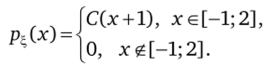
Определив величину константы С, найти и построить плотность и функцию распределения. Найти математическое ожидание М?, дисперсию Db, вероятность Р{^² < 1}.

Решение. Найдем константу С, используя свойство 2 плотности вероятности:

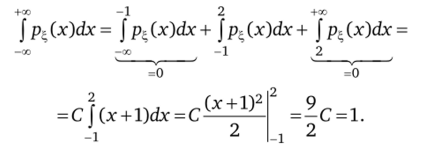
Отсюда С —.

Плотность распределения имеет вид.

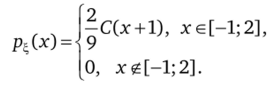
Функция распределения равна.

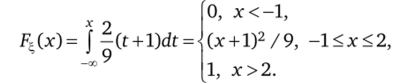
Графики плотность и функция распределения представлены на рис. 6.7.

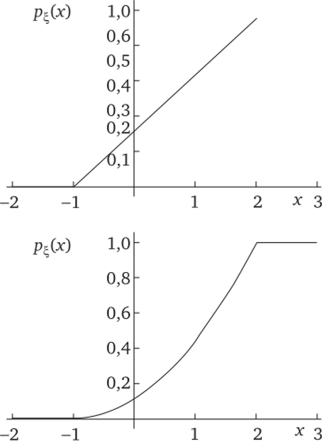
Рис. 6.7. Плотность распределения (а) и функция распределения (б) к задаче 6.1.

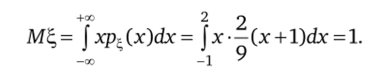
Дисперсия.

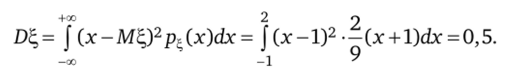
Вероятность.

Задача 6.2. Время уборки одного помещения распределено по равномерному закону на отрезке [5; 15] мин. Какова вероятность того, что время уборки каждого из трех помещений отклонится от математического ожидания не более чем на 4 мин?

Решение. Плотность равномерного распределения (х) = ——— = 0,1.

Среднее совпадает с математическим ожиданием и равно =10

мин. Вероятность того, что время уборки одного помещения отклонится от среднего не более чем на 4 мин, есть

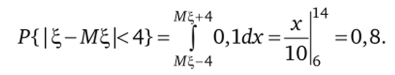
Каждое из трех помещений будет убрано с вероятностью отклонения от математического ожидания не более чем на 4 мин: (Р{ | - М% < < 4})³ = 0,512.

Задача 6.3. Срок службы батарейки имеет показательное распределение с математическим ожиданием 20 ч. Найти вероятность того, что батарейка проработает это время безотказно.

Решение. Если время работы устройства до выхода его из строя соответствует показательному закону, то случайная величина ?, есть длительность времени его работы. Вероятность того, что время безотказной работы окажется меньше t ч, равна Р (?, < 1) = РДО = 1 — е~Х‘. Вероятность того, что батарейка проработает не менее t ч, есть

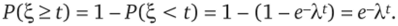
Математическое ожидание показательного распределения.

откуда X = 0,05.

Вероятность того, что батарейка проработает не менее 20 ч, равна.

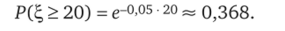
Величина е~Х¹ имеет название функции надежности. Она позволяет найти вероятность безотказной работы устройства в течение времени t при известном математическом ожидании.

Задача 6.4. Пусть случайная величина ?, имеет некоторую непрерывную возрастающую функцию распределения R (x). Доказать, что другая случайная величина ц, связанная с первой зависимостью r| = F_n(^), имеет равномерное распределение на отрезке [0; 1].

Решение. Если ?, < х и г| < у, то у = F-Qc) и х = F"¹ (у).

Найдем функцию распределения случайной величины Г|:

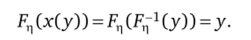
Очевидно, что у е [0; 1], т. е. случайная величина ц имеет равномерное распределение на отрезке [0; 1] и ее функция распределения может быть окончательно записана в виде.

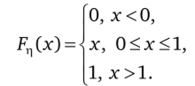
Задача 6.5. Случайная величина? имеет распределение Рэлея с плотностью.

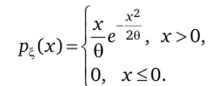
Найти математическое ожидание М?.

Решение. В соответствии с определением математическое ожидание случайной величины Е, равно.

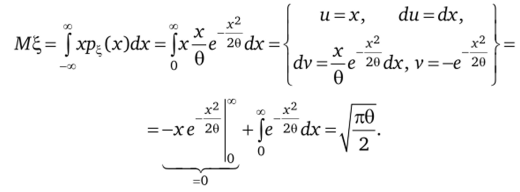
Задача 6.6. Показать, что случайная величина распределенная.

1 / Я по закону Коши с плотностью р_?(х)=-—, где х е К, не имеет матема;

1 + х²

тического ожидания.

Решение. Доказательство сводится к определению, существует ли определенный интеграл:

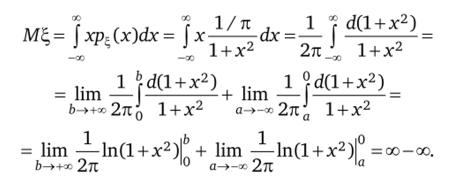
Математическое ожидание не существует. Если бы только один из интегралов обращался в бесконечность, а другой являлся бы конечной величиной, то математическое ожидание было бы равно +ос или —оо.

Задача 6.7. Для телефонного обслуживания сотрудников в офисе требуется мини-АТС. Каждый из них занимает номер в среднем 10 мин в час. Сколько каналов должна иметь телефонная станция, чтобы возможность потери вызова из-за перегрузки не отличалась от технической вероятности сбоя в линии, равной 0,003.

Решение. Каждый абонент либо разговаривает по телефону, либо нет. Имея дело с испытаниями Бернулли, воспользуемся формулой Муавра — Лапласа. Пусть случайная величина Е, — число абонентов на связи, т — наибольшее число абонентов, при котором линия связи еще работает. Вероятность того, что число абонентов ?, меньше т, равна.

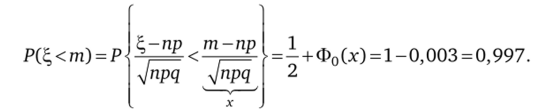
Отсюда получим ^=2Е- = х = 05'(0,497) = 2,750, что позволяет найти т: V*P.

m =пр+ 2,750y/npq =100- —+2,750. 100? — «26,9.

6 V 6 6.

Следовательно, если предусмотреть для линии связи 30 каналов, вероятность отказа по причине перегрузки не превысит величины 0,003.

Задача 6.8. Какова вероятность получить значение случайной величины ?, в пределах интервала Р{ |?,—а|, если Е, ~ Ш (а, а²)? Рассмотреть частные случаи: а) а = а = О, (3 = о = 1; б) а = МЪ_> = е°⁺ 2, а = 0, (3 =.

п² _ ,;

а = 1; в) а = М^ = е^а+ 2, р = = vе^2а(e^2cf2 -е°²), а = 0, ст = 1.

Решение. Воспользуемся формулой вероятности для логнормального распределения.

_ч 1 _т Ппх-сЛ

««<*)=₅₊ф"[—}.

Общая формула вероятности случайной величине ?, попасть в заданный интервал равна.

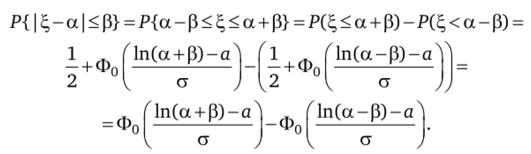
Частные случаи.

а) a = a = О, Р = a = 1. Имеем.

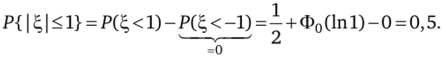
_а+ст²

б) а = М^ = е 2 _га = 0, (3 = а=1. Имеем.

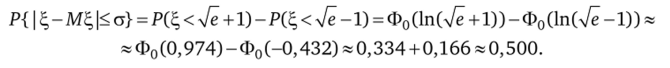
а² _ ,;

в) а = М^ = е°⁺ 2, р = = yjе^2а(е^2а2 -е°²), а = 0, ст = 1. Имеем.