Теория ZF-аксиоматическая теория множеств Цермело-Френкеля

Теория ZF была разработана в начале XX века и опубликована в 1908 году (см. [1], [15], [83], [86]). Излагаемая ниже система аксиом этой теории достаточно полна, чтобы получить из нее все обычные утверждения теории множеств, и в то же время позволяет избежать известных парадоксов.

• 1. Аксиома объемности: два множества А и В равны тогда и только тогда, когда они состоят из одних и тех же элементов.^[1]
• 2. Аксиома пары: если А и В — множества, то существует множество С, единственными элементами которого являются А и В: С = {А, В}.
• 3. Аксиома пустого множества: существует множество 0 — пустое множество, не содержащее элементов.
• 4. Аксиома объединения: если М есть множество некоторых множеств М_п т. е. М = {М, Л/₂, …}, то объединение UМ, — этих множеств М,•

есть множество.

• 5 .Аксиома степени: если М- множество, то совокупность Р (М) всех подмножеств множества М есть множество. Множество Р (М) называется степенью множества М.
• 6. Аксиома регулярности: если М- множество, то либо М = 0, либо в М найдется такой элемент b, что b П М = 0.
• 7. Аксиома содержательности: если М -множество и ф (х) — высказывательная форма языка теории, то совокупность D всех таких а е М, что ср (а) — истинное высказывание, есть множество, так что D = {a: (р(а)~ И, аеМ}. Множество D называется частью множества М, определяемой высказывательной формой (р (х).
• 8. Аксиома бесконечности: существует по крайней мере одно бесконечное множество, например: N= {0,1, 2,3,…}.
• 9. Аксиома выбора: для каждого множества А непустых множеств

А_{, /е/, A = {jAj, существует инъективная функция f:I^>A, сопостав;

ляющая каждому i е / элемент a_i = /(/) е А_г

Последняя аксиома не всегда включается в список аксиом теории множеств, хотя в теории множеств есть много эквивалентных ей утверждений (см. [36.0.24, 25]), а в анализе она часто присутствует в доказательствах неявно (см. [29]). Мы это иллюстрировать нс будем, но докажем три теоремы.

Теорема 3.3. Существует одноэлементное множество {А}.

• В аксиоме пары положим В = А , тогда.

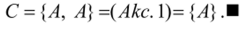
Теорема 3.4. Пусть, А — множество, тогда, А € А.

• Если /4 = 0, тогда по Аксиоме 3 А? А. Пусть А*0, тогда к множеству {А}- одноэлементному множеству, которое существует по Теореме 3.3, применим Аксиому регулярности 6, по которой ЗЬ е {А} такой, что b П {А} = 0. Поскольку {А} есть одноэлементное множество и is {А}, то b — А по Акс. 1. Теперь из А П {А} - 0 следует, что А

Теорема 3.5. Если, А и В суть множества и если, А е В, то В € А.

• • Для доказательства вновь обратимся к Аксиоме регулярности, применив ее к множеству {А, В), по этой аксиоме 3b е {А, В} ф 0 такой, что 6П {А, В) = 0.
• 1. Пусть b = В, тогда В П {А, В) = А (ибо по условию теоремы А е В и по Теореме 3.4 В&В). Далее пусть 1а): А = 0. Тогда по Аксиоме 3 В Условие 16) А*0 противоречит Аксиоме 6. Значит,
• 2. b = А, тогда по Аксиоме 6 А П {А, В} = 0, т. е. В g А. ?

Мы убедились в том, что аксиома регулярности избавляет теорию ZF от парадокса Б. Рассела.

• [1] Из аксиомы объемности вытекают такие два свойства множества: 1) если имеется множествоМ= {а, Ь} и некоторое выражение с переменной F (x), то после подстановки вместо х элемента, а из Мсамо множество М нс изменится, 2) {а, а, b}={a, b).