Методические рекомендации к изучению параллельности на плоскости

Часть рекомендаций по изучению отношений параллельности и перпендикулярности на плоскости и в пространстве была сформулирована выше. Дополним эти рекомендации еще рядом замечаний.

Прежде всего следует выполнить классификацию взаимного положения прямых в пространстве и на плоскости, используя в качестве модели каркас куба, поскольку свойства этой фигуры известны ученикам из курса математики 1—6-х классов. Рассматривая взаимное положение ребер куба, целесообразно познакомить учеников со скрещивающимися прямыми. В качестве иллюстрации можно использовать изображения многоуровневых транспортных развязок. В 7—9-х классах введение скрещивающихся прямых позволит мотивировать необходимость включения в определение параллельных прямых их принадлежность плоскости. Естественно, что ученики могут и самостоятельно сформулировать определение параллельных прямых, известное им из курса математики 5—6-х классов.

Основным материалом при изучении параллельности прямых являются признаки и свойства параллельных прямых и теорема о сумме углов треугольника. Строя изучение этих вопросов в логике конкретного учебника, следует внимательно отнестись к доказательству первого признака параллельности. Мы можем рекомендовать учителю разобрать со школьниками текст, приведенный в учебнике, составить план доказательства, выделить обоснования для каждого шага в доказательстве, что позволит естественным путем обнаружить пробелы в доказательстве (если таковые имеются) и устранить их. Поскольку доказательства других признаков обычно сводятся к первому из приведенных в учебнике, работу с ними целесообразно построить либо в логике самостоятельного поиска обоснования учениками, либо на основе изучения текста учебника. Первый вариант предпочтительнее, поскольку он способствует обучению поиску решения задач на основе либо нисходящего анализа, либо восходящего. Закрепление признаков и свойств параллельных прямых целесообразно при выполнении заданий по готовым чертежам (они в большом количестве представлены в различных изданиях учебника А. Д. Александрова). Кроме того, ученикам следует рекомендовать самостоятельно составить аналогичные задания. Изучая обоснования свойств параллельных прямых, следует раскрыть суть косвенного доказательства (доказательства «от противного»), если эго не было сделано ранее при изучении признаков равенства треугольников, еще раз обратить внимание школьников на связь прямой и обратной теорем. Тогда свойства параллельных прямых естественным образом возникнут как утверждения, обратные признакам параллельности.

Важным вопросом в теме является и изучение аксиомы параллельности. Ее следует рассматривать не только как основу для обоснования свойств параллельных прямых, но и как основу для содержательного обсуждения аксиоматического построения геометрии, знакомства с различными геометриями и начала серьезного знакомства с историей геометрии (историей математики) как научной системы и ее ролью в истории цивилизации.

Эффективно организовать самостоятельную работу учеников при изучении суммы углов треугольника можно на основе следующего задания.

Задача 17.3.

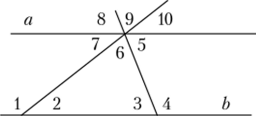
Рис. 173.

На рис. 17.3 прямые а и b параллельны. Какие из занумерованных углов будут равны? Пусть Z.2 = 40', Z8 = 50°. Величины каких углов можно определить? Какие теоретические выводы о сумме внутренних углов треугольника можно сделать? Как связаны между собой внешние и внутренние углы треугольника? Как, пользуясь теоремой о сумме углов треугольника, можно установить сумму углов выпуклого четырехугольника, выпуклого многоугольника?

Результатом работы с данным заданием станут теоремы о сумме углов треугольника и многоугольника и теорема о связи внешнего угла треугольника и его внутренних углов.

Как мы уже отмечали выше, в качестве дополнительного материала при изучении данной темы можно рассмотреть параллелограмм и трапецию.

Ввести понятие параллелограмма и познакомиться с его свойствами можно при работе над соответствующими заданиями.

Задача 17.4.

На рис 17.4 отрезки АК и MD пересекаются в точке О, их общей середине. Их концы последовательно соединены отрезками. Укажите на рисунке равные треугольники, равные углы. Каково взаимное расположение противоположных сторон образовавшегося четырехугольника? Знаете ли вы его название?

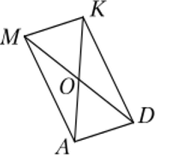
Рис. 17.4.

Это задание, с одной стороны, является упражнением по теме «Признаки параллельности прямых», а с другой — теоремой существования параллелограмма.

Свойства параллелограмма могут появиться как продукт выполнения следующего задания.

Задача 17.5.

На рис. 17.5 изображен четырехугольник, противоположные стороны которого параллельны. На рис. 17.5, а /-М = 40°. Определите углы этого четырехугольника. Чему будет равна их сумма? Какова связь противоположных углов этого четырехугольника?

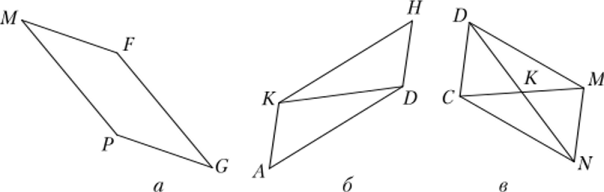
Рис. 17.5.

Изменится ли последний результат, если мы зададим другую величину угла?

Па рис. 17.5, 6 и в назовите равные углы, равные треугольники, равные отрезки. Какие свойства нарисованных четырехугольников вы можете сформулировать?

Вспомните, как называются четырехугольники на рис 17.5? Сформулируйте их свойства в виде утверждений со словами «Если …, то …». Проведите доказательства.

Данное задание также имеет двойное назначение. Оно является упражнением по теме «Свойства параллельных прямых», а также позволяет получить и обосновать основные свойства параллелограмма.

Если в материал данной темы включить еще и теорему Фалеса, теорему о средней линии треугольника, то это позволит существенно обогатить заданный материал, расширить возможности самостоятельной познавательной деятельности школьников.