Основные принципы страхования и актуарных расчетов

Рассмотрим основные принципы, на которых базируются современные страхование и актуарные расчеты.

I. Принцип случайности. Как мы уже отмечали, страховаться могут только такие риски, которые обладают признаками случайности и вероятности их наступления.

Страхуются только чистьте риски (рис. 1.1).

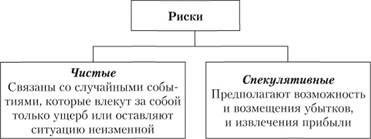
Рис. 1.1. Виды страховых рисков.

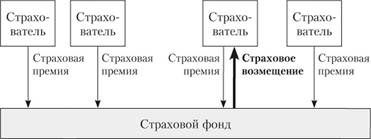
Рис. 1.2. Солидарная и замкнутая раскладка ущерба в страховом фонде.

II. Принцип солидарной и замкнутой раскладки случайных убытков. Для страхования характерна замкнутая раскладка ущерба (рис. 1.2) в рамках создаваемого страхового денежного фонда^[1]. Средства фонда расходуются только для компенсации ущерба его участников. Таким образом, страхование основано на предпосылке, что количество страхователей, попавших в страховой случай, существенно меньше общего количества участников, регулярно выплачивающих взносы в страховой фонд. Страхователь имеет право на возмещение только при наступлении страхового случая.

Мы уточним эту схему в гл. 2 (см. рис. 2.2), когда введем структуру страховой премии.

Страховые фонды образуются исключительно на основе перераспределения денежных доходов и накоплений, образующихся в процессе первичного распределения национального дохода. Это делает страхование особо восприимчивым к тенденциям экономического развития (инфляция, снижение темпов экономического роста и др.) и отличает его от других финансовых отраслей экономики.

III. Принцип пространственных и временных границ.

Этот принцип состоит в соблюдении строго оговоренных в договоре страхования пространственных и временных границ страховой защиты объекта страхования. С ним связана еще одна особенность страхования — перераспределение wiu выравнивание ущерба по территории и во времени^[2]. Динамика ущерба не затрагивает в равной мере все территориальные единицы. Это обстоятельство увеличивает возможности раскладки ущербов и расширяет возможности страхования, особенно страховых компаний с развитой филиальной сетью. Неравномерность ущербов во времени порождает необходимость резервирования части страховых платежей для возмещения чрезвычайных ущербов в неблагоприятные годы или периоды года. Это особенно важно в страховании крупных рисков типа космических, энергетических и т. п.

IV. Принцип коллективного баланса. Этот актуарный принцип тесно связан с теорией вероятностей, математической статистикой и свойствами суммарного распределения случайных величин. Страхование основывается на том, что объединение (коллектив, портфель) нескольких рисков, имеет более выгодное распределение убытка и размер премии (в расчете на один полис), чем каждый отдельный риск, поскольку в коллективе благоприятные и неблагоприятные (по сравнению с математическим ожиданием риска) процессы убытков отдельных рисков могут взаимно комненсироваться^[3]. Более подробно мы разберем этот принцип в гл. 2.

ПРИМЕР 1.1^[4]

Страховая компания страхует автомобили от угона (фиксированный ущерб) на полную стоимость С = S = 20 тыс. у.е. В портфеле компании 10 000 таких независимых однородных договоров, вероятность наступления страхового случая оценивается страховой компанией как 0,01. Чему равно математическое ожидание и среднее квадратическое отклонение выплат: а) по одному договору; б) но всему портфелю суммарно и в расчете на один договор.

Решение

а) рассмотрим один договор.

Так как ущерб фиксирован, то выплаты страховой компании при наступлении страхового случая будут составлять страховую сумму, т. е. 20 тыс. у.е., а распределение случайной величины — выплат страховой компании по одному договору (У) — будет иметь вид:

		S
	<1	Р

Математическое ожидание Y:

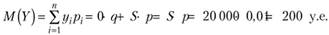
Таким образом, средний ожидаемый размер выплат по одному договору составляет 200 у.е.

Дисперсия Y:

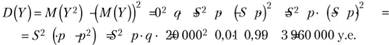
Среднее квадратическое отклонение Y:

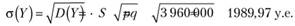
Как мы видим, среднее квадратическое отклонение почти в 10 раз превышает математическое ожидание ущерба.

б) рассмотрим портфель из п= 10 000 таких договоров, собранный компанией.

Риски предполагаем по условию независимыми и одинаково распределенными, поэтому по свойству математического ожидания и дисперсии суммы независимых случайных величин имеем.

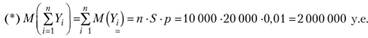
Математическое ожидание суммарного ущерба по портфелю из 10 000 таких договоров увеличилось в 10 000 раз и составило 2 млн у.е.

Распределение числа страховых случаев, наступающих в таком портфеле, имеет биномиальное распределение и результат (*) можно было получить другим способом. Среднее число страховых случаев, наступающих в таком портфеле, равно М (т) = пр, по каждому случаю выплачивается страховая сумма S, поэтому.

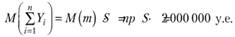
Аналогично дисперсия суммы независимых случайных величин равна сумме дисперсий, следовательно.

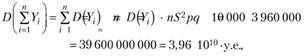
а среднее квадратическое отклонение суммарного ущерба по портфелю возрастет нев 10 000 раз, как математическое ожидание и дисперсия, а в 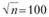раз:

Если же посчитать эти характеристики па один договор, то видим, что математическое ожидание риска на один договор не изменилось:

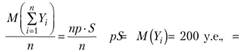
а среднее квадратическое отклонение суммарного риска, приходящееся на один договор, уменьшилось в 100 раз:

И теперь суммарное среднее квадратическое отклонение, приходящееся на один договор, почти в 10 раз меньше математического ожидания.

Из примера мы увидели, в чем состоит утверждение Томаса Мака^[5], составляющее принцип коллективного баланса: " Объединение (коллектив, портфель) нескольких рисков имеет более выгодное распределение убытка и размер премии (в расчете на один полис), чем каждый отдельный риск" .

V. Принцип эквивалентности. Принцип эквивалентности обязательств страховщика и страхователя^[6] — основной принцип всех актуарных расчетов — выражается в равенстве математических ожиданий двух величин: суммы всех страховых взносов и суммы всех страховых возмещений. Именно из этого условия определяется размер основной составляющей страховой премии — рисковой премии (подробно см. в гл. 2).

Этот принцип тесно связан с принципом замкнутой раскладки ущерба. Страховая эквивалентность состоит в том, что, в конечном счете, все взносы (за исключением части страховой премии, предназначенной на ведение дела и прибыль — нагрузки), полученные страховой компанией (СК) от клиентов, за тарифный период (существенно зависящий от вида страхования, например, 5 лет), вернутся к страхователям в виде страховых выплат. Риск угрожает многим лицам, но только немногие попадут в страховые случаи.

Теоретической базой для главного принципа актуарных расчетов — принципа эквивалентности служит один из фундаментальных законов теории вероятностей — закон больших чисел.

Согласно закону больших чисел, а именно теореме Чебышева^[7], при достаточно большом числе п независимых случайных величин, дисперсии которых ограничены некоторым числом, среднее арифметическое этих величин стремится по вероятности к среднему арифметическому их математических ожиданий:

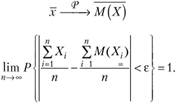
А если говорить об однородных рисках с одинаковым математическим ожиданием М (Х), то среднее арифметическое всех рисков стремится по вероятности к математическому ожиданию ущерба по данному виду страхового договора (частный случай теоремы Чебышева):

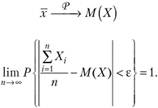
Таким образом, согласно закону больших чисел:

• 1) математическое ожидание ущерба в одном договоре — справедливая цена за принятие такого рода случайных рисков. Поэтому рисковую премию (РП) (см. главу 2) вычисляют как математическое ожидание выплат страховщика М (Y);
• 2) требуется собрать как можно бо? льшую группу независимых однородных рисков (для выполнения условий наилучшего приближения закона больших чисел).

За исключительно важную роль для коллективного баланса и исчисления страховых премий закон больших чисел теории вероятностей часто называют фундаментальным законом страхования.

• [1] Федорова Т. А. Основы страховой деятельности. М.: БЕК, 2002.
• [2] Федорова Т. А. Указ. соч.
• [3] Мак T. Математика рискового страхования: пер. с нем. М.: ОлимпБизнес, 2005.
• [4] Прообраз задачи см.: Корнилов И. А. Основы страховой математики. М.: ЮНИТИ-ДА II А, 2004.
• [5] Мак Т. Математика рискового страхования: иер. с нем. М.: ОлимпБизнес, 2005.
• [6] Корнилов И. А. Указ. соч.
• [7] Вентцель E. С. Теория вероятностей. М.: КноРус, 2010; Мхитарян В. С., Астафьева Е. В., Миронкина Ю. Н., Трошин Л. И. Теория вероятностей и математическая статистика / под ред. В. С. Мхитаряна. М.: Изд-во МФПА, 2011.