Кредитное рационирование. 
Макроэкономика.

Коммерческий банк выдает кредиты и ищет такую ставку кредита, которая обеспечит максимум его прибыли. Проблема состоит в том, что при увеличении ставки растет прибыль, получаемая от одного заемщика, но вместе с тем сокращается число самих заемщиков, поскольку для некоторых из них повышенная ставка не выгодна. Таким образом, решается необычная задача максимизации суммы показателей в условиях, когда число слагаемых является переменной величиной.

Кредитное рационирование — выбор банком ставки кредита, которая максимизирует прибыль в условиях, когда число заемщиков банка зависит от ставки кредита: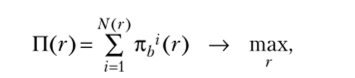

где П — суммарная прибыль банка; n_h‘® — возрастающая функция прибыли банка, полученной от г-го заемщика; г — ставка кредита; N® — убывающая функция количества заемщиков банка.

Пусть имеется несколько предпринимателей, которые реализуют проекты с равными инвестициями В и равным ожидаемым доходом R, но с разной степенью риска. В случае успеха г-й предприниматель получает доход Rf в случае неудачи — Rf (одинаковая для всех величина). Вероятность успеха — p_v неудачи — (1 — р,). Считаем, что с увеличением номера проекта растет вероятность успеха. Для всех проектов выполняется.

Преобразуем это равенство:

Отсюда следует, что чем больше вероятность успеха проекта, тем меньше доход предпринимателя в случае успеха: поскольку все проекты в среднем имеют равный доход, увеличение одного «позитивного» фактора неизбежно влечет сокращение другого.

Банк выдает кредит в размере В но своей ставке г при условии, что при успехе предприниматель выплачивает кредит с процентами (1 + г)В, а при неудаче — сумму Rf, при этом:

В случае неудачи прибыль предпринимателя равна нулю, так как весь свой доход Rf он отдает банку, поэтому ожидаемая прибыль равна.

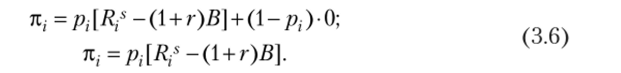
Из (3.5) следует, что ожидаемая прибыль каждого предпринимателя больше нуля. Подставим R,^s из (3.4) в (3.6), получим прибыль предпринимателя как функцию вероятности успеха:

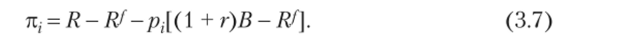
Из неравенства (3.5) следует, что ожидаемая прибыль предпринимателя убывает с ростом p_iy т. е. фактор снижения дохода с ростом вероятности успеха проекта оказался решающим.

Нормальная прибыль (я₀) — минимальная прибыль предпринимателя, ниже которой реализация любого проекта невыгодна.

Отсекающая вероятность (р) — максимальная вероятность успеха предпринимательского проекта, при которой прибыль не опускается ниже нормального уровня при заданном ожидаемом доходе проекта. Отсекающей вероятности соответствует отсекающий (максимальный) номер проекта N. Для всех реализуемых проектов выполняется.

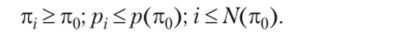
Ожидаемая прибыль банка от i-го заемщика без учета фактора дисконтирования равна ожидаемому доходу за вычетом суммы кредита:

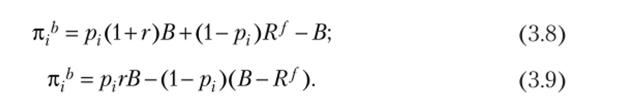
Отсюда следует, что прибыль банка от одного заемщика растет линейно с ростом ставки. Суммарная прибыль банка от N заемщиков:

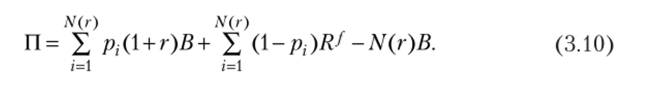
Исследуем изменения слагаемых в правой части (3.10) с ростом г:

• • первое может расти из-за роста г или снижаться из-за снижения N;
• • второе снижается из-за снижения N, что влечет снижение прибыли;
• • третье слагаемое отрицательное, его модуль снижается из-за снижения N, что влечет рост прибыли.

Имеются девять проектов: р, = 0,1; R = 3; Rf = В = 2. В табл. 3.3 значения R* рассчитаны по формуле (3.4), а значения к, при ставках 10% и 20% — по формулам (3.6) и (3.8). Исследована прибыль банка при трех значениях минимальной прибыли и двух ставках процента. Если я_ц = 0,95, то при ставке 10% прибыль больше, чем при 20% (0,06 > 0,04). Если я₀ = 0,91, то при ставке 10% прибыль также больше (0,2 > 0,12). Если я₀ = 0,71, то при ставке 10% прибыль меньше (0,9 < 1,12). Итак, существует некое значение минимальной прибыли предпринимателя, при которой банк получает одинаковую прибыль при ставках 10% и 20%.

Таблица 33

Кредитное рационирование: прибыль при разных ставках кредита.

Частный случай. Имеется М проектов, а = 1 / М; р, = а г, RJ = В. Тогда из (3.4) и (3.6) следует.

Получим приближенное (нецелое) значение отсекающего номера проекта, приравняв прибыль ее требуемой величине:

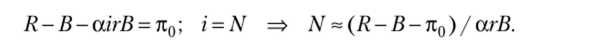
Сверхприбыль проекта (71)) — ожидаемый доход проекта за вычетом издержек (суммы кредита) и нормальной прибыли (п_х = R — В — л₀). Тогда для рассматриваемого частного случая отсекающий номер проекта равен.

Отсюда следует, что все М проектов будут выгодны, если сверхприбыль проекта превышает выплаты по кредиту (n_t > гВ). В противном случае будет реализована лишь часть проектов.

Из (3.9) получим формулу прибыли банка от одного заемщика и общую прибыль банка в случае, когда г < л, / В и реализуются все М проектов. Используем формулу суммы арифметической прогрессии:

Отсюда следует, что при низких ставках кредита прибыль банка растет пропорционально ставке кредита. При высоких ставках кредита, когда г> к, / В, реализуются N проектов и прибыль банка равна.

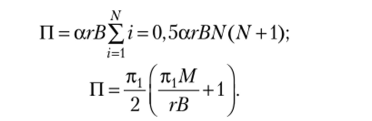
Отсюда следует, что при высоких ставках кредита прибыль банка падает с ростом ставки кредита. Итак, оптимальная ставка кредита (г*) равна отношению сверхприбыли к сумме кредита, а максимальная прибыль банка (II*) приближенно равна половине суммарной сверхприбыли всех проектов:

Прибыль банка сначала растет линейно от нуля до максимального значения, а затем убывает по гиперболе с ростом ставки кредита:

Непрерывный случай. Имеется бесконечное множество предпринимателей, функция плотности распределения />, равна &{р,). Если р — отсекающая вероятность, то формула прибыли банка (3.9) примет вид.

Продифференцируем (3.12), учитывая, чтор зависит от г, и используя правило дифференцирования интеграла с переменным верхним пределом. Приравняем производную нулю:

Интеграл в правой части положителен, а второе слагаемое отрицательно, так как dp/dr < 0. Ставка кредита, которая удовлетворяет (3.13), оптимальна для банка.