Поведение в мире деформаций

Из отмеченных обстоятельств снова следует вывод о необходимости сближения двух соседних таких ДЕФОНОВ-ТОРОИДОВ сжатия, что равнозначно притяжению, подобно притяжению ДЕФОНОВ-СФЕРОИДОВ на рис. 20, но величина такого тяготения ДЕФОНОВ-ТОРОИДОВ находится в зависимости не только от расстояния между ними, но и от относительной друг друга пространственной ориентации: в экваториальных плоскостях… Читать ещё >
Поведение в мире деформаций (реферат, курсовая, диплом, контрольная)
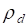
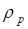
Назовём ДЕФОНОМ окрестность деформированной среды вокруг ЛОКАЛЬНОЙ ДЕФОРМАЦИИ в точке О с указанными компонентами нормальных и тангенциальных напряжений, поверхности которых показаны выше на рис. 6 рис. 7 и рис. 8. Ясно, что субстанция в мире деформаций обладает физическими свойствами, на которые мы не имеем никаких оснований распространять традиционные в физике наши представления (о плотности, температуре, вязкости, упругости и т. п.), поэтому вынуждены здесь пока этот вопрос оставить открытым. Можно лишь предположить пока, что эти свойства близки к свойствам физического вакуума, примерные представления о которых мы имеем по результатам инструментальных исследований ближнего космического пространства: температура близка к абсолютному нулю, вязкость соответствует сверхтекучести при сверхнизких температурах и т. п. При этом из отмеченного выше свойства совместности деформаций (см. рис. 4 по п. 2) ясно, что плотность субстанции в таком ДЕФОНЕ сжатия больше плотности субстанции в его окрестности, что можно графически представить некоторой зависимостью.
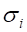
(8).
где от точки О, как это показано на рис. 17.
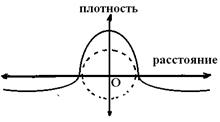
Рис. 17 (ВНУТРЕННИЙ или ВНЕШНИЙ), что непосредственно связано с радиусом кривизны соответствующей поверхности
Так как поведение таких ДЕФОНОВ определится направлениями указанных напряжений, то в этом вопросе должна быть полная определенность, обязывая нас рассмотреть его более подробно. Здесь уместно вспомнить, что понятие НАПРАВЛЕНИЯ в ГЕОМЕТРИИ определяется величиной УГЛА — величины, которая появляется лишь в двумерных мирах — поверхностях (радиан) и в трёхмерных мирах (стерадиан). При этом, если для если для однозначности величины плоского УГЛА необходимо указание его знака (правый — по часовой стрелке или левый — против часовой стрелки относительно заданного РЕПЕРА — линии), то для однозначности величины УГЛА пространственного ещё необходимо указание и его ориентации относительно поверхности.
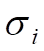
Для иллюстрации отмеченного обстоятельства воспользуемся результатами топологических исследований векторных полей на поверхностях [18] и др. Представим себе простейший такой сфероидный ДЕФОН сжатия в окрестности точки О как на рис. 18, тогда на рис. 19 получим изображение векторных полей нормальных (рис. 19-а) и тангенциальных (рис. 19-б) компонент напряжения в смежной со сфероидом окрестности, которые по определению ортогональны друг другу (см. рис. 19). (рис. 89-а) и б) по [18]).
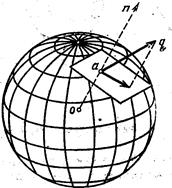
![(рис. 88 по [18]) Рис. 19 (рис. 89-а) и б) по [18]).](/img/s/9/33/2082733_8.jpg)
Рис. 18 (рис. 88 по [18]) Рис. 19 (рис. 89-а) и б) по [18])
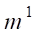
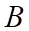
Вместе с этим, два подобных ДЕФОНА, расположенные вблизи друг от друга, окажутся с противоположных сторон любой поверхности, которые всегда могут быть представлены замкнутыми в бесконечности по несобственной линии вокруг любого из ДЕФОНОВ, как это наглядно показано на рис. 20, на котором — след пограничной поверхности между окрестностями ДЕФОНОВ и, имеющих характеристики и соответственно. Ясно, что радиус кривизны этой поверхности для ДЕФОНОВ и будет иметь противоположные знаки. Из отмеченных обстоятельств сразу следует необходимость сближения двух соседних таких ДЕФОНОВ — СФЕРОИДОВ сжатия, что равнозначно притяжению, как это показано на рис. 20, оставляя пока открытым вопрос о величине такого тяготения.
![(рис.186 по [18]).](/img/s/9/33/2082733_11.png)
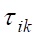
Разумеется, направления полей нормальных и тангенциальных компонент напряжения в смежных с другими нашими простейшими ДЕФОНАМИ окрестностями, имеющих поверхности тороида (рис.14) и скрученного тороида (рис.15) необходимо рассмотреть с этих позиций также подробно. Из одного того факта, что в отличие от односвязного сфероида тороид (см. рис.14) является двухсвязным [18], сразу следует вывод об отсутствии центральной симметрии векторного поля нормальных плоскости тороида, осевую симметрию, позволяя представить изменение векторного поля нормальных компонент напряжения, опуская математические преобразования, проделанные автором ранее [19], как на рис. 21, на котором обозначены штриховыми линиями n и — n предельные уровни значений векторного поля нормальных компонент напряжения.
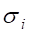
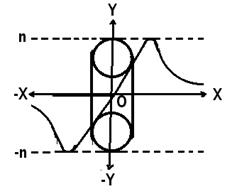
Рис. 21 Компонент напряжения, присущих сфероиду (см. рис. 18), приобретая в полярной плоскости, ортогональной экваториальной
Из отмеченных обстоятельств снова следует вывод о необходимости сближения двух соседних таких ДЕФОНОВ-ТОРОИДОВ сжатия, что равнозначно притяжению, подобно притяжению ДЕФОНОВ-СФЕРОИДОВ на рис. 20, но величина такого тяготения ДЕФОНОВ-ТОРОИДОВ находится в зависимости не только от расстояния между ними, но и от относительной друг друга пространственной ориентации: в экваториальных плоскостях их взаимодействие подчиняется центральной симметрии, подобно взаимодействия ДЕФОНОВ — СФЕРОИДОВ (см. рис.20), а в полярной плоскости взаимодействие ДЕФОНОВ-ТОРОИДОВ сжатия подчиняется осевой симметрии, также здесь оставляя пока вопрос о величине такого тяготения открытым. При этом здесь важно отметить действие отмеченной особенности взаимодействия ДЕФОНОВ-ТОРОИДОВ в отличие взаимодействия ДЕФОНОВ — СФЕРОИДОВ лишь, как это ясно из графической зависимости на рис. 21, на расстояниях между ДЕФОНАМИ-ТОРОИДАМИ, сравнимыми с их собственными размерами.
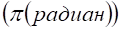
Представить строение, но не механизм образования ДЕФОНАскрученного ТОРОИДА (см. рис.15) из ДЕФОНА-ТОРОИДА (см. рис.14), ДЕФОНА — СКРУЧЕННОГО ТОРОИДА возможно по рис. 22-а), рис. 22-б) и рис.22-в), на которых показаны ДЕФОНТОРОИД (см. рис. 22-а) целый, ДЕФОН-ТОРОИД разрезан нормальной к его экватору плоскостью по А-В и торцы разреза развернуты относительно друг друга на 1800 (см. рис. 22-б), так что точки А2 и В1 поверхности ДЕФОНА-ТОРОИДА поменялись положением, то есть А2 заняла положение В1, а В1 заняла положение А2, в результате образуя ДЕФОН-СКРУЧЕННЫЙ ТОРОИД (см. рис. 22-в).
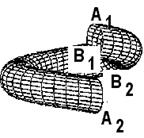
Рис. 22-а) Рис. 22-б) Рис. 22-в
В действительности образование ДЕФОНА-СКРУЧЕННОГО ТОРОИДА возможно представить как процесс движения окружности вокруг некоторой точки деформируемой среды по внешней оси — замкнутой траектории при вращении этой окружности относительно траектории движения центра этой окружности до замыкания траектории — являющейся осью ТОРОИДА. Как мы видели выше (см. рис.16), деформации кручения сопутствуют все остальные виды деформации: и сжатие, и растяжение, и сдвиг, и изгиб. Поэтому особый практический интерес для нас представляет та зависимость.
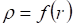
(8).
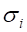
плотности от расстояния внутри самого ДЕФОНА-СКРУЧЕННОГО ТОРОИДА и в его окрестностях, как это нами было установлено для ДЕФОНА — СФЕРОИДА (см. рис. 17), и также зависимость векторного поля нормальных компонент напряжения в его окрестности, как это мы выше обнаружили для ДЕФОНА-ТОРОИДА (см. рис.14).
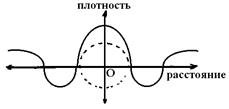
Рис. 23.
В соответствии с отмеченными «УСЛОВИЯМИ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ» Сен-Венана [7] совершенно понятно, что при кручении ДЕФОНА-ТОРОИДА (см. рис. 15-б) его поверхностный слой испытывает растяжение, которое при необходимости можно даже вычислить, сравнив длины винтовой линии от А1 до В2 или от А2 до В1 с длиной соответствующего экватора тороида (см. рис. 15-а). Данное обстоятельство приводит к необходимости деформации растяжения в ближайшей СКРУЧЕННОМУ ДЕФОНУ-ТОРОИДУ (см. рис. 15-в) окрестности как рис. 23. Кроме того, рассматривая упругие напряжения на самой поверхности такого скрученного тороида, показанные на рис. 24, где линии напряжений на поверхности скрученного тороида между и, также между и, наглядно показанные на рис. 25, непременно приведут вследствие статической реакции к свертыванию этого СКРУЧЕННОГО ДЕФОНА-ТОРОИДА, которую в плане можно изобразить на рис. 26, а представить его реальный вид снизу на рис. 27 и реальный вид сбоку на рис. 28.

Рис. 24 Рис. 25 Рис. 26
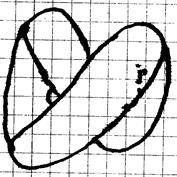

Рис. 27 Рис. 28
Другими словами, СКРУЧЕННЫЙ ДЕФОН-ТОРОИД образует своеобразную асимметричную СКОБУ, в окрестностях которой сопутствующие деформации образуют также асимметричную область, в пределах которой значения и направления нормальных и тангенциальных компонент напряжения отображают эту асимметричность окрестностей с различных сторон относительно СКОБЫ СКРУЧЕННОГО ДЕФОНА-ТОРОИДА. Из отмеченных обстоятельств снова следует вывод об асимметричности взаимодействия между собой СКОБ СКРУЧЕННОГО ДЕФОНА-ТОРОИДА и с другими ДЕФОНАМАМИ в зависимости не только от расстояний, но и от относительной друг друга пространственной ориентации. Кроме того, учитывая выше отмеченное обстоятельство, что понятие НАПРАВЛЕНИЯ в ГЕОМЕТРИИ определяется величиной и знаком УГЛА, приходится признать определяющее влияние на величину и направление взаимодействия также и НАПРАВЛЕНИЯ КРУЧЕНИЯ СКРУЧЕННЫХ ДЕФОНОВ-ТОРОИДОВ, которых может быть два: ПРАВОЕ или ЛЕВОЕ. Таки образом, оставляя пока вопрос о величине такого взаимодействия открытым, необходимо отметить важный вывод, что изменение размерности в мире деформаций приводит к изменению качества непрерывной субстанции (ЭФИРА), в частности, в мире деформаций это изменение от вида к виду деформации заключается в изменении симметрии взаимодействия ДЕФОНОВ между собой, сопоставляя которые с эмпирически известными взаимодействиями можно отметить соответствие этих взаимодействий известным типам симметрии [20]:
- 1. Центрально-симметричное взаимодействие — притяжеие.
- 2. Центрально-осевая симметрия взаимодействия:
- 2−1. Асимметричное взаимодействие в статике:
- 2−1-1. Отталкивание одноименных,
- 2−1-2. Притяжение разноименных.
- 3. Асимметричное взаимодействие в движении:
- 3−1-1. Отталкивание разноименных,
- 3−1-2. Притяжение одноименных.
- 4. Сцепление ДЕФОНОВ:
- 4−1.Сцепление ДЕФОНОВ со СКРУЧЕННЫМИ ДЕФОНАМИ:
- 4−1-1.Сцепление ДЕФОНОВ с правыми ДЕФОНАМИ,
- 4−1-2.Сцепление ДЕФОНОВ с левыми ДЕФОНАМИ.
- 4−2.Сцепление СКРУЧЕННЫХ ДЕФОНОВ между собой:
- 4−2-1.Сцепление правых ДЕФОНОВ между собой,
- 4−2-2.Сцепление левых ДЕФОНОВ между собой,
- 4−2-3.Сцепление правых ДЕФОНОВ с левыми.
Сопоставляя теперь обнаруженные выше виды взаимодействий в МИРЕ ДЕФОРМАЦИЙ с эмпирически известными взаимодействиями можно отметить соответствие этих взаимодействий известным в физике ПОЛЯМ:
- 1. ТЯГОТЕНИЕ ТЕЛ (ГРАВИТАЦИЯ) — Центрально-симметричное взаимодействие.
- 2. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ — Асимметричное взаимодействие в статике.
- 3. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ТОКОВ (МАГНИТНОЕ НАТЯЖЕНИЕ) — Центрально-осевая симметрия взаимодействия — Асимметричное взаимодействие в движении.
- 4. МОЛЕКУЛЯРНЫЕ СИЛЫ — сцепление СКРУЧЕННЫХ ДЕФОНОВ.
- 5. ЯДЕРНЫЕ СИЛЫ — Сцепление ДЕФОНОВ.
При этом распространение колебаний в окружающем МИРЕ ДЕФОРМАЦИЙ (ЭФИРЕ, содержащем ДЕФОНЫ) подчиняется законам ИЗЛУЧЕНИЯ.
4. Условие стабильности и виды взаимодействий в мире деформаций:
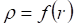
![Исходя из отмеченного выше свойства совместности деформаций (см. рис. 4 по п. 2) ясно, что зависимости плотности эфира в ДЕФОНЕ и его окрестностях по (8), представленные нами выше на рис. 10 и рис. 16, смогут существовать лишь в стационарных условиях, когда внешние причины поддерживают указанные величины и направления полей нормальных и тангенциальных компонент напряжения, показанных выше на рис. 12. Так как мы пока не указали никаких таких причин поддержания условия по (8) , то ожидать выполнения взаимодействий по известным типам симметрии [20] у нас нет никаких оснований. Другими словами, при отсутствии внешних причин для сохранения условия по (5) наши ДЕФОНЫ должны распространиться на всю окрестность, то есть расшириться до исчезновения полей нормальных и тангенциальных компонент напряжения. Подобную ситуацию образно описал ещё Дж.А. Уилер [21]: «…Представим себе тёмные пятна, передвигающиеся по поверхности озера в поле зрения наблюдателя, смотрящего с высокой башни. О н изучает их движение достаточно тщательно, чтобы вывести уравнения движения и закон эффективных сил, действующих между этими «пятнами». Кроме того, из других исследований ему известны законы гидродинамики жидкости в озере. В один прекрасный день, воспользовавшись новым биноклем большей разрешающей силы, он увидит, что «пятна» вообще не являются чуждыми объектами. Они являются вихрями в среде, свойства которой он уже знает. Тогда он возвращается к уравнения гидродинамики и выводит из них законы движения завихрений и их взаимодействия. Это даёт гораздо более глубокое понимание увиденного…» Подобно Дж.А. Уилеру посмотрим сверху на реку. Для этого наблюдения прекрасно подходит наша Ангара: на поверхности реки турбулентности постоянно образуют завихрения, воронки и тому подобные образования струй потока реки. Теперь продолжим наблюдение Дж.А. Уилера, прослеживая за одним определенным таким новообразованием на поверхности потока: вот возник вихрь, маленький завиток струй с маленькой ямочкой внутри и чёткими границами, далее он «плывёт» по течению, расширяясь, контуры его теряются, плавно переходя в поверхность потока, а далее это новообразование уже невозможно различить на поверхности потока, оно «исчезло»?! Однако, на поверхности реки снова возникают другие турбулентные «объекты» - вихри, которые так же плывут, расширяются, размываясь в потоке, и так непрерывно по всей поверхности потока реки! Посмотрим же теперь на поверхность стоячей воды, например, в ближайшем пруду, даже в заливе реки, но там на поверхности воды мы не увидим никаких «объектов» турбулентности, никаких завихрений, поэтому там и исчезать, размываться нечему.](/img/s/9/33/2082733_28.png)
Исходя из отмеченного выше свойства совместности деформаций (см. рис. 4 по п. 2) ясно, что зависимости плотности эфира в ДЕФОНЕ и его окрестностях по (8), представленные нами выше на рис. 10 и рис. 16, смогут существовать лишь в стационарных условиях, когда внешние причины поддерживают указанные величины и направления полей нормальных и тангенциальных компонент напряжения, показанных выше на рис. 12. Так как мы пока не указали никаких таких причин поддержания условия по (8), то ожидать выполнения взаимодействий по известным типам симметрии [20] у нас нет никаких оснований. Другими словами, при отсутствии внешних причин для сохранения условия по (5) наши ДЕФОНЫ должны распространиться на всю окрестность, то есть расшириться до исчезновения полей нормальных и тангенциальных компонент напряжения. Подобную ситуацию образно описал ещё Дж.А. Уилер [21]: «…Представим себе тёмные пятна, передвигающиеся по поверхности озера в поле зрения наблюдателя, смотрящего с высокой башни. О н изучает их движение достаточно тщательно, чтобы вывести уравнения движения и закон эффективных сил, действующих между этими „пятнами“. Кроме того, из других исследований ему известны законы гидродинамики жидкости в озере. В один прекрасный день, воспользовавшись новым биноклем большей разрешающей силы, он увидит, что „пятна“ вообще не являются чуждыми объектами. Они являются вихрями в среде, свойства которой он уже знает. Тогда он возвращается к уравнения гидродинамики и выводит из них законы движения завихрений и их взаимодействия. Это даёт гораздо более глубокое понимание увиденного…» Подобно Дж.А. Уилеру посмотрим сверху на реку. Для этого наблюдения прекрасно подходит наша Ангара: на поверхности реки турбулентности постоянно образуют завихрения, воронки и тому подобные образования струй потока реки. Теперь продолжим наблюдение Дж.А. Уилера, прослеживая за одним определенным таким новообразованием на поверхности потока: вот возник вихрь, маленький завиток струй с маленькой ямочкой внутри и чёткими границами, далее он «плывёт» по течению, расширяясь, контуры его теряются, плавно переходя в поверхность потока, а далее это новообразование уже невозможно различить на поверхности потока, оно «исчезло»?! Однако, на поверхности реки снова возникают другие турбулентные «объекты» — вихри, которые так же плывут, расширяются, размываясь в потоке, и так непрерывно по всей поверхности потока реки! Посмотрим же теперь на поверхность стоячей воды, например, в ближайшем пруду, даже в заливе реки, но там на поверхности воды мы не увидим никаких «объектов» турбулентности, никаких завихрений, поэтому там и исчезать, размываться нечему.
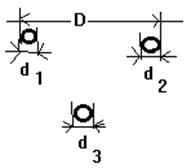
Ситуацию сохранения стационарности условия (5) возможно представить, например, при расширении окружающей исследуемые ДЕФОНЫ окрестности по аналогии расширения самих ДЕФОНОВ. Из данного обстоятельства можно заключить, что самосохранение условия стабильности взаимодействия ДЕФОНОВ обязано расширению окружающей среды вместе с расширением самих ДЕФОНОВ! Это значит, что свойство расширения окружающей ДЕФОНЫ среды (эфира) является АТРИБУТОМ данной среды, содержащей данные ДЕФОНЫ, то есть неотъемлимым свойством данного МИРА ДЕФОРМАЦИЙ (ЭФИРА). Другими словами, ДЕФОНЫ по описанному выше представляют собой подсистемы некоего внешнего по отношению к ним НАД-ДЕФОНА что может быть логически продолжено неопределенно многократно, как, например, это наглядно показано на рис. 22-а), рис.22-б) и рис. 22-в), а реально может быть осуществлено в расширяющемся из одно центра О мире, пример которого показан на рис. 23, на котором ДЕФОНЫ A B и C размерами d на расстоянии D друг от друга, например, по оси абсцисс, сохраняют отношение этих параметров в различных положениях, пронумерованных индексами 1, 2 и 3 соответственно.
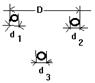
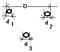
Рис.29-а) Рис. 29-б Рис. 29-в
Геометрия такого процесса известна и описана в винтовом исчислении [22] Котельникова А. П., к сочинениям которого я здесь отсылаю читателя. Лучевое пространство по — Котельникову А. П. [22] практически реализуется в известном «красном» смещении, сущность которого можно иллюстрировать словами Стивена Хокинга из его «Краткой истории времени» [23], один абзац со стр. 62 ниже сканирован для предотвращения кривотолков и недоразумений:


Рис. 30.
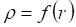
Таким образом, в лучевом пространстве расширяющегося мира ДЕФОНЫ с плотностью эфира по (8), представленные выше на рис. 10 и рис. 16, в сущности являются волнами-частицами, которые в 1924 году Луи де-Бройль открыл для микромира [24], а в 1986 году Чечельницкий А. М. [25] обнаружил для мегамира: «…С позиций представлений о волновой Вселенной в рамках концепции волновой астродинамики установлены довольно точные значения физических характеристик межпланетной среды — космической плазмы, подтверждаемые данными наблюдений…». В продолжение и подтверждение этих соображений необходимо здесь отметить длинный ряд эмпирических и экспериментальных результатов, которые на протяжении всего XX века находились под пристальным вниманием физиков мира, доклады некоторых только на одной Конференции в честь 100-летия А. Эйнштейна «Проблемы физики: классика и современность» в 1979 году здесь без цитирования можно назвать: «Понятие Геометрии» Акицуку Кавагути [26], «Эйнштейн и обснование квантовой теории» Франка Кашлюн [27], «Доклад о парадоксе Эйнштейна-Подольского-Розена» Жан-Пьера Вижье [28] и др. При внимиательном рассмотрении с изложенных позиций можно обнаружить, что известные парадоксы и внутренние противоречия КВАНТОВОЙ МЕХАНИКИ, СТО и ОТО, других современных теорий [23], [24], [25] - являются ЭМПИРИЧЕСКИМИ И ЭКСПЕРИМЕНТАЛЬНЫМИ ОСНОВАНИЯМИ изложенных выше идей и принципов СТЕРЕОХРОНОДИНАМИКИ (СХД). Так, напри мер, парадокс ЭПР в сущности является отражением на квантово-механическом уровне опыта Козырева Н. А по упреждению положения звезды [29] и др.