Свойства деревьев. 
Деревья как частный вид графов

Сформулируем основные свойства деревьев.

Свойство 1.

Для каждой пары вершин дерева существует единственный путь, их соединяющий.

Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов. Например, на рисунке (являющегося деревом, вершины которого изображены прямоугольниками с помещенной в них информацией) представлено генеалогическое дерево некоего Максима.

Рис. 17

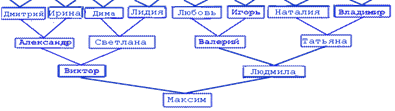
По этому дереву однозначно находится предок Максима в любом поколении по любой линии.

Свойство 2.

Всякое ребро в дереве является мостом. Действительно, после удаления любого ребра дерева, оно «распадается» на два дерева.

Рис. 18

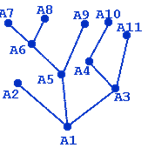
Это легко видеть на рисунке, если удалить, например, ребро А5А6 или ребро А1А3, или ребро А4А10 (оставив «вторым деревом» вершину A10).

Теорема.

Дерево с n вершинами имеет n-1 ребро.

Доказательство.

Для дерева — изолированной вершины n=1 и ребер 0, что соответствует теореме (n—1 = 1—1 = 0). Если из графа «дерева», не являющегося изолированной вершиной, удалить одно ребро, то получается два дерева с теми же вершинами. Для получения трех деревьев нужно удалить два ребра; для получения четырех деревьев — три ребра и т. д. Наибольшее количество деревьев из графа с n вершинами можно получить n (n изолированных вершин), чего можно достичь, удалив n—1 ребро. ч. т. д.

Задача. В стране Древляндия 101 город, и некоторые из них соединены дорогами. При этом любые два города соединяет ровно один путь. Сколько в этой стране дорог?

Решение.

Из условия задачи следует, что граф дорог Древляндии — дерево. У этого дерева есть висячая вершина. Удалим ее вместе с ребром, которое из нее выходит. Оставшийся граф также является деревом. Поэтому у него есть висячая вершина, которую мы также удалим вместе с выходящим из нее ребром. Проделав эту операцию 100 раз, мы получим граф, состоящий из одной вершины (в котором, конечно, нет ребер). Поскольку каждый раз удалялось ровно одно ребро, то сначала их было 100.

Теперь рассмотрим остальные свойства деревьев. Сделаем это в виде совокупности утверждений, которые эквивалентны между собой (т.е. из любого утверждения следует любое другое).

Теорема 1. Пусть G (X, E) — неориентированный граф с p вершинами и q ребрами. Тогда следующие утверждения эквивалентны.

• 1. G есть дерево.
• 2. Любые две различные вершины x и y графа G соединены единственной простой цепью.
• 3. G — связный граф, утрачивающий это свойство при удалении любого из его ребер.
• 4. G — связный граф и:

p = q + 1.

5. G — ациклический граф и:

p = q + 1.

6. G — ациклический граф, причем если любые две его вершины x и y соединить ребром e, то в полученном графе будет ровно один простой цикл.

Для доказательства теоремы достаточно доказать следующую цепочку следствий: 1 > 2 > 3 > 4 > 5 > 6 > 1, так как это означает, что из любого утверждения 1 — 6 выводится любое другое.

• 1 > 2. Так как граф связен, то любые две его вершины можно соединить простой цепью. Пусть 1 и 2 — две различные простые цепи, соединяющие вершины x и y. Если цепи 1 и 2 не имеют общих вершин, за исключением вершин x и y, то есть простой цикл. Предположим, что цепи 1 и 2 имеют общие вершины, отличные от x и y. Пусть z — первая из таких вершин при движении от вершины x к вершине y и пусть 1 (x, z) и 2 (x, z) — части цепей 1 и 2, взятые от вершины x до вершины z. Тогда — простой цикл. Это противоречит тому, что граф ацикличен, и поэтому 1=2, т. е. утверждение 2 доказано.
• 2 > 3. Граф G — связен, поскольку любые две его различные вершины x и y соединены простой цепью. Возьмем некоторое ребро графа e = (x, y). Согласно 2 простая цепь ={e} между вершинами x и y единственна. Если ребро e удалить, то вершины x и y будет невозможно соединить простой цепью, и полученный граф будет несвязным. Утверждение 3 доказано.
• 3 > 4. По условию 3 граф связен. Соотношение:

p = q + 1.

докажем по индукции. Если граф имеет две вершины и удовлетворяет 3, то он выглядит так:

Рис. 19

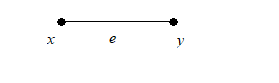
В этом случае p = 2, q = 1 и соотношение:

p = q + 1.

выполняется. Предположим теперь, что соотношение верно для всех графов, удовлетворяющих 3 и имеющих меньше, чем p вершин, и докажем его для графа G с p вершинами. Удалим из графа G произвольное ребро e. Тогда новый граф G? будет несвязным и будет состоять из двух связных компонент G1 и G2. По предположению индукции имеем:

p1 = q1 + 1,.

p2 = q2 + 1,.

где pi — число вершин компоненты Gi, qi — число ее ребер. Следовательно,.

p = p1 + p2,.

q = q1 + q2 + 1,.

поэтому:

p = q1 + q2 + 2 = q + 1,.

и свойство 4 доказано.

4 > 5. Предположим, что граф G, удовлетворяющий 4, имеет простой цикл длиной 1. Этот цикл содержит l вершин и l ребер. Для любой из p — l вершин, не принадлежащих циклу, существует инцидентное ей ребро, лежащее на кратчайшей цепи (т. е. цепи минимальной длины), идущей от данной вершины к некоторой вершине цикла. Все такие ребра попарно различны. Если вершины x1 и x2 инцидентны одному такому ребру e, то e = (x1, x2), и кратчайшая цепь 1 для вершины x1 проходит через вершину x2, а кратчайшая цепь 2 для вершины x2 проходит через вершину x1 (рис. 20). Это противоречит тому, что цепи 1 и 2 — кратчайшие. Общее число ребер q в графе G в этом случае не меньше, чем:

l + p — l = p,.

т. е. q = p, что противоречит соотношению:

p = q + 1.

Отсюда следует, что G — ациклический граф, и утверждение 5 доказано.

Рис. 20

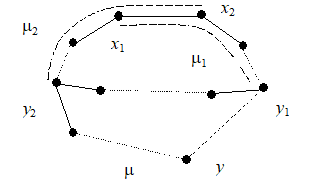
5 > 6. Так как G — ациклический граф, то каждая его компонента связности Gi (i = 1, 2, …, k) является деревом. Для каждой компоненты Gi имеем в соответствии с 5:

pi = qi + 1,.

откуда:

.

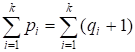
т. е.:

p = q + k.

С другой стороны:

p = q + 1,.

поэтому k = 1, т. е. граф G связен. Таким образом, G — дерево. Тогда (см. 2) любые две различные вершины x и y графа G соединены единственной простой цепью. Если добавить ребро между несмежными вершинами x и y, то оно образует с указанной цепью единственный простой цикл. Утверждение 6 доказано.

6 > 1. По условию 6 G — ациклический граф. Если граф G не является связным, то возьмем вершины x и y из различных компонент связности графа G и соединим их ребром e. Построенный граф является, как и граф G, ациклическим. Это противоречит свойству G, поэтому G — связный граф, и свойство 1 доказано. Таким образом, доказана и теорема 1.

Определение, аналогичное дереву, можно ввести и для орграфа.

Определение 2. Орграф G (X, E) называется прадеревом или ориентированным деревом, растущим из корня x0, при следующих условиях:

• 1. Неориентированный граф G', соответствующий графу G, является деревом.
• 2. Единственная простая цепь между x0 и любой другой вершиной x графа G' является путем в орграфе G, идущим из вершины x0 в вершину x.

На рис. 21 изображено ориентированное дерево.

Рис. 21

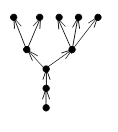
В неориентированном графе G (X, E) вершина x называется концевой или висячей, если d (x) = 1, т. е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.

Теорема 2. В любом дереве G (X, E) с p * 2 вершинами имеется не менее двух концевых вершин.

Доказательство. Пусть q — число ребер дерева G. В силу теоремы 1:

p = q + 1.

Кроме того, из теоремы 1.1 имеем:

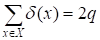
Таким образом, получаем:

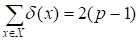
.(1).

Предположим, что x0 — единственная концевая вершина в дереве G. Тогда (x0) = 1, (x) 2, если x0. Отсюда:

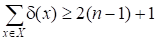
.(2).

Неравенство (2) противоречит (1), поэтому либо концевых вершин нет, либо их по крайней мере две. Если концевых вершин в G нет, то (x) 2 для всех X. Тогда:

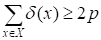
.(3).

Неравенство (3) тоже противоречит (1). Отсюда следует, что концевых вершин в G две или больше. Теорема доказана.

Важным является вопрос о том, сколько существует деревьев с заданным числом вершин. Для деревьев с помеченными вершинами (например пронумерованными) или для помеченных деревьев ответ на этот вопрос дает следующая теорема.