Рациональность. 
Обучение учащихся рациональным способам решения задач

Рациональность. Рациональные способы решения математических задач Огромная значимость нахождения школьниками различных способов решения задач по математике не раз отмечалась на страницах методической литературы. Однако наблюдения показывают, что на уроках, как правило, рассматривается лишь один из способов решения задачи, причем не всегда рациональный. Приводимая в таких случаях аргументация в виде отсутствия достаточного количества времени на решение одной задачи различными способами не имеет под собой основы: для математического развития учащихся гораздо полезнее одну задачу решить несколькими способами (если это возможно) и не жалеть на это времени, чем несколько однотипных задач одним способом. Из различных способов решения одной и той же задачи необходимо предложить учащимся выбрать наиболее рациональный, красивый, простой [14].

По мнению Фрейда, рационализация возникает, когда человек, не осознавая истинную причину своих действий, заменяет ее на другую, достаточно логичную и нетравмирующую, а потому более приемлемую для Эго. Ярким примером рационализации является известная басня Крылова «Лиса и виноград». Лиса, желающая полакомиться виноградом, наталкивается на непреодолимое препятствие — «висят они высоко: хоть видит око, да зуб немеет». Чтобы снять конфликт, Лиса прибегает к рационализации: «Ну что ж! На взгляд-то он хорош, да зелен — ягодки нет зрелой: тотчас оскомину набьешь» [20].

С точки зрения философии рациональность трактуется, как разумный, отправляющийся от разума, осуществляющий благодаря разуму, целесообразный, практический, вполне осмысленный [29].

Д. Пойа писал, что действие или суждение является рациональным, если оно основано на ясных, обозримых доводах, а не возникает из таких туманных источников, как привычка, впечатления, ощущения или «вдохновения». Утверждение, которое мы возводим в ранг математической теоремы после кропотливого и критического изучения его доказательства, — вот прототип рационального суждения. С известной точки зрения главная польза изучения математических доказательств состоит в том, что они ближе всего подводят нас к той идеальной рационалистической манере, мыслить, которая более всего приличествует человеку, homo sapiens, «разумному существу» [23].

Неясно, однако, в чем именно должна заключаться рациональность действий решающего. Практика показывает, что имеются хорошие шансы на то, что предварительное продумывание строго формулируемых соображений может оказать благотворное влияние на его интуицию, на смутные его ощущения, — и описанный образ действий, видимо, надо считать наиболее рациональным.

Как бы там ни было, решающий должен научиться сохранять равновесие между смутными ощущениями и ясными доводами. Возможно, что это — самое важное из того, чему он должен научиться. Д. Пойа сформулировал правило, которым должен руководствоваться решающий:

Никогда не идите наперекор своим ощущениям, но старайтесь также трезво взвесить все аргументы за и против ваших планов [23].

Из этого высказывания можно сформулировать некоторые пожелания (напутствия) ученикам при решении задач:

никогда впопыхах, сходу не пытайся решить задачу, это может привести к нежелательному результату;

сначала подумай, найди другие варианты решения задачи;

выбери наиболее рациональный, оптимальный для тебя [см. приложение 2.].

Рациональные способы решения задач — это наиболее простые, красивые способы решения [14].

При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки [12]. После нахождения очередного способа решения задачи учащийся, как правило, получает большое моральное удовлетворение. Поэтому учителю важно поощрять поиск различных способов решения задач, а не стремиться навязывать свое решение.

Самое сложное в организации решения задач разными способами — это помощь учителя в нахождении этих способов. При этом учитель должен выступить не с идеей нового варианта решения, а с вопросом или серией вопросов, инициирующих появление соответствующей идеи или идей. Это не простое дело, и ему нужно учиться. Сложность связана с тем, что эта деятельность учителя направлена не на применение некоторого знания или приема, а на развитие воображения или интуиции ученика [5].

Бонтянский В. Г. и Груденов Я. И. работали над проблемой поиска различных способов решения задач и написали статью «Как учить поиску решения задач» [3], они показали основные затруднения, которые возникают у учащихся и предложили некоторые рекомендации, которые способствуют более быстрому отысканию способов решения задач.

Также над данной проблемой работала Зайцева Г. Д., которая написала статью «О решении задач различными способами» [9], Крайзман М. Л. его статья называется «Решение задач различными способами» [15] и др.

Рассматривая решение задач несколькими способами, учитель на уроке должен ориентировать учащихся на поиски красивых, изящных решений. Тем самым учитель будет способствовать эстетическому воспитанию учащихся и повышению их математической культуры.

Рощина Н. Л. в своей статье «Решение задач различными способами — первый шаг к эстетическому восприятию геометрии» [25], показала эффективность решения задач различными способами. Она сделала вывод, что благодаря различным способам решения задач у учащихся повышается интерес к предмету: «никто из учеников не остается равнодушным, дети начинают смотреть на геометрию не как на сухую скучную науку, а видят, что и здесь нужны выдумка, фантазия, творчество».

Решая с учащимися ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая — помочь ученику решить именно данную задачу, научить его решать задачи, аналогичные рассматриваемой; вторая — так развить способности ученика, чтобы он в будущем смог решить любую задачу школьного курса самостоятельно. Поэтому, преследуя вторую цель, при решении задач несколькими способами следует обратить внимание учащихся на наиболее рациональный, красивый способ решения данной задачи.

Решение одной задачи несколькими способами, и нахождение рационального способа, имеет большое значение для математического развития учащихся, чем решение однотипных задач.

Методика обучения учащихся рациональным способам решения математических задач.

Обучение рациональным способам решения задач нужно вести таким образом, чтобы обучить учащихся общим приемам рациональных решений.

Пак И. И. в статье «Приемы рационализации вычислений как средство развития мышления учащихся» [21], рассказывает, что существуют общие приемы рациональных решений, на основе которых решаются многие задачи и благодаря которым у учащихся развиваются различные формы мышления.

Рассмотрим наиболее общие приемы рациональных способов решения математических задач.

Прием отыскания рациональных способов решения, используя теоретический материал и систему предшествующих упражнений.

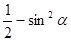
Например. Преобразовать в произведение выражение .

Данный пример можно решить так:

.

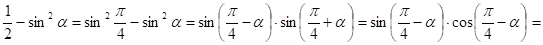
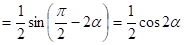
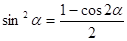
Но если перед решением данного примера, ввести формулу, то первый пример можно решить гораздо проще:

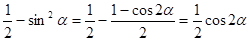
. Т. е. на выбор решения влияет система упражнений, предшествующих решаемому примеру или задаче.

Готман Э. Г. в статье «Поиск рационального решения задачи на экстремум» показал, что на выбор решения влияет ранее изученный теоретический материал. Например, при нахождении экстремумов функций, не всегда рационально использовать производную, гораздо проще находить экстремумы на основе свойств функций [4].

Все основные положения о влиянии теоретического материала и системы предшествующих упражнений на выбор способа решения предложенной задачи имеют место и при решении геометрических задач.

Если, например, при изучении теоремы Пифагора предложить задачу на вычисление длины некоторого элемента прямоугольного треугольника, то учащиеся ищут решение только с применением этой теоремы, т. е. отсутствует связь с предыдущим материалом.

Решая задачи и примеры определенного типа, учащиеся постепенно создают себе правила о едином подходе к их решению. В результате появляется формальный, почти механический подход, что снижает ценность решения соответствующих задач и примеров [17].

Например, при решении квадратных уравнений ах2 + bx + c = 0, когда, а есть дробное число, учащиеся всегда предварительно приводят к общему знаменателю, ибо решение уравнения с целыми коэффициентами для них легче, чем с дробными, хотя коэффициенты при этом усложняются. Но если 4ас будет целым числом, то значительно проще решать уравнение без освобождения от знаменателя.

Поэтому необходимо не только поощрять, но и разъяснять с помощью специально подобранных примеров целесообразность отступления в конкретных случаях от схемы решения. Надо приучать учащихся указывать из нескольких возможных решений то, которое скорее и проще других ведет к цели.

Например, нередки случаи, когда учащиеся для отыскания корней квадратного уравнения (х — а)(x — b) = 0 раскрывают скобки и применяют формулу корней квадратного уравнения. Мы считаем, что в подобных недочетах виноват учитель. Если бы с учащимися основательно разобрали решение уравнений методом разложения на множители, то таких нерациональных решений учащиеся не допускали бы [17].

Необходимо показать учащимся метод устного нахождения корней квадратных уравнений по теореме Виета, который значительно облегчает и решение уравнений, сводящихся к квадратным, а также решение задач на составление квадратных уравнений.

Иногда, учитель сам того не замечая, приучает учащихся к нерациональным методам решения. Например, изучая системы уравнений, в которых неизвестные входят в знаменатели дробей и, делается вывод, что проще такую систему решить методом введения вспомогательных неизвестных.

Этот вывод ошибочен, так как, например, системы вида.

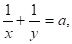
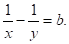
проще всего решать устно, складывая и вычитая почленно эти уравнения.

Введение

вспомогательных неизвестных оправдано при решении более сложных систем, где применение устных вычислений для большинства учащихся затруднительно.

Прием отыскания рациональных способов решения алгебраических задач составлением уравнений.

Обычно в таких задачах за исходные неизвестные принимают те величины, которые требуется определить. Но решение многих задач упрощается при более удачном выборе неизвестных величин.

Многие задачи по алгебре могут быть решены как составлением одного уравнения с одним неизвестным, так и составлением системы уравнений с несколькими неизвестными. В большинстве случаев составление системы уравнений значительно проще, чем составление уравнения с одним неизвестным, но решение системы сложнее, чем решение уравнения. Поэтому при оценке простоты решения нужно сравнивать, насколько составление системы уравнений проще, чем составление уравнения, и в какой степени это упрощение компенсирует усложнение вычислений.

Кроме того, существует ряд задач, решение которых чисто арифметическими методами изящнее и проще, чем с помощью уравнений.

В качестве примера рассмотрим задачу: «Два мотоцикла выехали одновременно из пунктов, А и В навстречу друг другу и встретились в 50 км от В. Прибыв в пункты, А и В, мотоциклы сразу же повернули назад и встретились вновь в 25 км от А. Сколько километров между, А и В?».

Решение этой задачи с помощью уравнения представляет для учащихся определенные трудности: не случайно в школьном учебнике аналогичная задача помещена в разделе «Задачи повышенной трудности».

Гораздо легче решить эту задачу, не составляя уравнения, а рассуждая так. От начала движения до первой встречи оба мотоциклиста проехали вместе расстояние, равное АВ, а к моменту второй встречи проехали вместе втрое большее расстояние. Таким образом, каждый из них до второй встречи проехал втрое больше, чем до первой. Мотоциклист, выехавший из пункта В, до первой встречи проехал 50 км. Следовательно, до второй встречи он проехал 150 км (50•3=150). Поэтому расстояние от, А и В равно 125 км (150−25=125).

При таком походе эту задачу могут решить учащиеся не только VIII, но и V класса.

Прием отыскания рациональных способов решения задач, используя тождественные преобразования.

В таких заданиях обычно требуется упростить выражение или же найти его значение, при этом рациональность решения зависит от формулировки самого задания.

Например, если в задании сначала сказано упростить выражение, а затем найти его числовое значение, то не всегда решение будет рациональным, т. к. иногда удобнее сразу подставить числовые значения.

Но есть задания без указания на необходимость предварительного упрощения исходного алгебраического выражения, то в этом случае нужно выяснить, следует ли преобразовывать алгебраическое выражение или же сразу заменить все буквы их числовыми значениями.

Для упрощения тождественных выражений используются формулы сокращенного умножения, тригонометрические формулы, метод вынесения общего множителя за скобки, метод группировки и др.

Решение большинства задач сводится к последовательному решению отдельных простых задач. Ответы на промежуточные задачи используются как данные величины при решении последующих задач, что значительно упрощает решение данной задачи. Таким образом, можно выделить еще один прием нахождения рациональных способов решения, который основывается на промежуточных задачах.

Например, определить объем конуса, зная его высоту Н и боковую поверхность S. Для решения этой задачи не обязательно находить радиус основания конуса, достаточно найти его квадрат, что несколько упрощает решение. Так как в задаче исходные величины заданы в общем виде, то нет необходимости в ответе и в промежуточных вычислениях заменять р его числовым значением. Иногда в задачах гораздо проще в промежуточных выкладках выражать определяемые величины через р, не подставляя его числовое значение.

Рациональность зависит от формы записи решения арифметических и алгебраических примеров. Рассмотрим два способа записи решений: 1) отдельно по действиям; 2) последовательными преобразованиями, цепочкой.

Решение цепочкой состоит в том, что решение представляется в виде последовательно расположенных тождественных преобразований, причем действия, требующие громоздких выкладок, выполняются отдельно от основных записей, а все остальные выполняются устно. Такое решение будет рациональным, если почти все действия можно выполнить устно. Если же, например, для выполнения каждого действия нам понадобиться переписать весь пример, то даже и в случае отсутствия действий, требующих записей в стороне от основных, решение цепочкой будет менее рациональным, чем решение по действиям [17].

Для упрощения решений большое значение имеют формулы. Более того, введение некоторых из них мотивируется необходимостью упрощения вычислений и преобразований. Поэтому следующий прием рациональных решений, который мы рассмотрим, основывается на применении формул.

Например, квадратное уравнение можно решить выделением полного квадрата, но такие решения довольно сложны и громоздки. Так для уравнения x2 + px + q = 0 целесообразней применять общую формулу для нахождения корней уравнения:

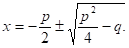
Аналогичные примеры можно привести и из других разделов школьного курса математики.

Каждую из формул cos2x=cos2x — sin2x=1 — 2sin2x=2cos2x — 1 учащиеся всегда могут вывести, но знание этих формул в готовом виде не только упрощает выполняемые преобразования, но и сокращает время, а в некоторых случаях помогает найти план решения.

Большое значение имеет, и умение устно преобразовывать известную формулу, чтобы получить вспомогательные формулы, т. к. очень часто решение упрощается при применении несколько преобразованной формулы. Например, применение известной формулы куба суммы двух чисел в виде (а + b)3 = a3 + b3 + 3ab (a + b) значительно упрощает решение многих алгебраических и тригонометрических упражнений.

В действующих учебниках алгебры и начала анализа можно заметить, что основные формулы представлены на форзацах, это значительно облегчает восприятие и запоминание формул учащимися. В учебнике «Алгебра и начала анализа 10−11», Мордковича А. Г. после каждой главы выделяется отдельный параграф, в котором представлены все основные формулы и понятия, для структурирования и обобщения изученного материала.

Благодаря формулам решение многих задач значительно упрощается, но существуют и такие утверждения, которые способствуют отысканию рациональных способов решения задач. Такие утверждения называются вспомогательными, которые в большей степени используются на уроках геометрии.

Рассмотрим, лемму о подобии треугольников. На основании этой леммы доказываются все признаки подобия треугольников, она используется и при изучении темы «подобные многоугольники».

Так же при решении геометрических задач нередко значительно рациональнее установить подобие треугольников ссылкой на лемму, чем на один из признаков подобия треугольников.

Нужно обращать внимание учащихся на те утверждения, которые в учебнике даже не выделены в виде отдельной леммы, но знание, которых имеет большое значение в отыскании рациональных решений.

Рассмотрим еще один прием рациональных решений, в основе которого лежит метод вспомогательных неизвестных.

Очень часто выбор вспомогательных неизвестных достаточно сложен и непонятен, и от того какую величину мы обозначим за неизвестную, зависит рациональность решения задач. В этом случае учителю необходимо просто подсказать учащимся, какую величину целесообразно принять за неизвестное.

Например, найти четыре последовательных целых числа, произведение которых равно а.

Можно за неизвестное х принять наименьшее из них, тогда получим уравнение:

х (х + 1)(х + 2)(х + 3) = а, т. е. х4 + 6×3 + 11×2 + 6х — а=0.

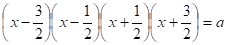
Если же обозначить буквой х среднее арифметическое искомых чисел, то получим биквадратное уравнение, которое решается легко.

В таких случаях нужно подсказать учащимся, какую величину целесообразно принять за неизвестное, чтобы получить более простое решение.

В геометрии аналогом вспомогательных неизвестных являются вспомогательные (дополнительные) построения. Иногда достаточно построить вспомогательную прямую, отрезок или другую какую-либо фигуру, чтобы найти простейшее решение предложенной задачи.

Также следует отметить не только рациональные способы решения задач, но и рациональную запись решения. Далингер В. А. в своей книге «Обучение учащихся доказательству теорем» [6], показывает две формы рациональной записи доказательства теорем. Одна из них состоит в том, что в начале записывается вывод, а рядом аргументы, на основе которых был сделан вывод. Другая форма предполагает заполнение таблицы, состоящей из двух столбцов: шаги доказательства и обоснование шагов.

Рассмотренные нами примеры дают более общие представления о рациональных способах решения задач. Но нельзя конкретно говорить, что именно данный прием относится к этому классу задач, так как многие задачи решаются по-своему, могут сочетать в себе несколько приемов. Поэтому жесткие границы между приемами поставить нельзя, так же как не следует забывать, что существует множество частных приемов рациональных решений, которые подходят только для отдельных задач, некоторые из них основываются на знаниях из смежных дисциплин.