Лекция №7. Адсорбция на поверхности твердых тел

Твердые тела обладают способностью адсорбировать из окружающей среды на своей поверхности молекулы, атомы или ионы. Процессы адсорбции на твердой поверхности аналогичны процессам адсорбции на жидкой поверхности, т. е. на поверхности твердого адсорбента адсорбируются твердые вещества, понижающие поверхностное натяжение его относительно окружающей среды.

Очевидно, что при прочих равных условиях для данных адсорбента и адсорбата, адсорбция будет тем больше, чем больше поверхность адсорбента. Поэтому хорошими адсорбентами могут быть материалы, обладающие сильно развитой поверхностью, имеющие сильно пористую, губчатую структуру, или материалы, находящиеся в состоянии тонкого измельчения.

Из применяемых в практике адсорбентов первое место принадлежит различным видам специально изготовленных адсорбционных углей (древесный, кровяной, костный и др.). Они могут обладать исключительно развитой поверхностью пор. Так, 1 г активированного угля обладает внутренней поверхностью пор, достигающей 400−900 м². Кроме активных (активированных) углей в качестве адсорбентов применяются такие вещества как селикогель, кремнезем, каолин и др.

Явление капиллярной конденсации Твердый адсорбент может содержать поры в виде узких каналов диаметром порядка 10^-7 см, т. е. капилляры. В таких капиллярах кроме обычной адсорбции, может происходить капиллярная конденсация паров. Если жидкость хорошо смачивает стенки капилляра, то мениск ее всегда бывает выгнутым. В этих условиях давление насыщенного пара будет более низким, чем над плоской поверхностью, насыщение паров и их конденсация будет происходить раньше чем достигается состояние насыщения (точка росы) для большой плоской поверхности. Пары будут конденсироваться в жидкость в капиллярах. Такое явление получило название капиллярной конденсации. Многие родные и искусственные материалы (почвы, рыхлые известняки, уголь и др.) обладают сильно развитой системой капилляр и пор. В них способны конденсироваться пары воды или других жидкостей, не являющихся насыщенными к обычной плоской поверхности.

Адсорбция из растворов Изотермы адсорбции растворенных веществ из растворов аналогичны изотермам адсорбции газов (изотерма Ленгмюра), но адсорбция из растворов, являющихся многокомпонентными системами, осложняется одновременной адсорбцией растворенного вещества и растворителя. (уравнение адсорбции Гиббса d=-d_iГ_i).

Рассмотрим адсорбцию вещества из бинарных растворов (растворитель — В, растворенное вещество — А).

Для состояния адсорбционного равновесия можно записать такое уравнение:

А+(В)(А)+В, где, А и (А) — молекулы растворенного вещества в объеме раствора и на адсорбенте; В и (В) — молекулы растворителя в объеме раствора и на адсорбенте.

Как для всякой химической реакции константа равновесия (К) определяется выражением:

.

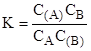
Если концентрацию, А и В выразить в мольных долях, то есть общее число молей в растворе N=A+B, и общее число молей на адсорбенте (N)=(A)+(B), тогда А/N+В/N=1 или N_A+N_B=1, и (N_A)+(N_B)=1. Соответственно константа адсорбционного равновесия равна.

.

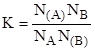
Выражая N_В=1-N_A и (N_В)=1-(N_A), получим.

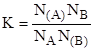
откуда.

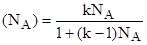
. (1).

Это выражение (1) представляет собой уравнение изотермы адсорбции из бинарного раствора. Проанализируем его:

если Na0, т. е. концентрация растворенного вещества мала, то (N_A)кN_A, т. е. это уравнение Генри.

Если Na1, т. е. раствор состоит почти из растворенного вещества (N_A0 — растворителя почти нет), то (N_A) 1, т. е. в адсорбционном слое почти одно вещество А.

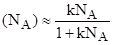
Если вещество, А сильно адсорбируется на адсорбенте, то К1 и — это уравнение подобно уравнению Ленгмюра.

Если вещество, А слабо адсорбируется на адсорбенте, то К1 и.

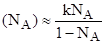
Это выражение показывает, что мольная доля вещества, А на поверхности адсорбции мала при любых Na и начинает быстро возрастать лишь при N_A1.

На рассмотренном примере, адсорбция растворенного вещества, А выражается величиной (N_A), а график изотермы адсорбции вещества, А на поверхности адсорбента (N_A)=f (N_A) будет выглядеть так:

• 1 — так выглядит зависимость (N_A)=f (N_A), если вещество, А сильно адсорбируется на поверхности адсорбента;
• 2 — при слабой адсорбции вещества, А на поверхности адсорбента;
• 3 — при средней адсорбции вещества, А на поверхности адсорбента, т. е. когда адсорбция растворенного вещества, А и растворителя В примерно одинаковы (следует иметь в виду, что на поверхности адсорбента при любом значении Na в растворе «свободные места» заняты молекулами растворителя на веществе А, но в различных соотношениях).

В практике химиков-энергетиков явление адсорбции встречаются в химанализе (газовая, жидкостная, ионообменная хромотография), а главным образом в процессах ионного обмена, при коагуляции и обезмасливание конденсата и паров.

Сущность процесса ионного обмена. Основные понятия

Процесс ионного обмена представляет собой адсорбцию электролитов. В частности в процессах водоподготовки на ТЭС — адсорбцию сильных электролитов (солей) при обессоливании природной воды. Такой процесс адсорбции электролитов происходит из воды на поверхности раздела: вода — полярное твердое вещество. Сам процесс адсорбции получил название ионного обмена, а адсорбент — твердое вещество — ионита.

Механизм, происходящих при этом явлений, таков. При адсорбции ионов одного какого-нибудь знака поверхность твердой фазы принимает заряд этих ионов, а раствор — противоположный по знаку в результате наличия в нем избытка ионов, противоположных знаку заряда адсорбированных ионов.

Это создает разность потенциалов между раствором и твердой фазой как следствие обуславливает притяжение ею ионов противоположного знака заряда (противоионов), находящихся в растворе.

На противоионы действуют силы:

Сила электростатического притяжения со стороны твердой фазы.

Диффузионные силы, под действием которой противоионы имеют тенденцию статистически распределиться по всему объему. Действие этих сил приводит к тому, что вокруг твердой фазы образуется диффузионный слой ионитов или ионная атмосфера. (см. рис.). Ионы, адсорбированные твердой фазой (+) носят название потенциалообразующих ионов, ионы, образующие ионную атмосферу. (-), носят названия ионов диффузного слоя.

Ионы диффузного слоя называют противоионами, т.к. они имеют заряд, противоположный адсорбированным ионам.

Ионы диффузного слоя, обладающие повышенным запасом кинетической энергии, могут вырываться из ионной атмосферы и переходить в раствор. Из раствора в ионную атмосферу могут поступать ионы того же знака в эквивалентном количестве.

Таким образом, в процессе адсорбции ионов можно различить три составляющих момента:

возникновение заряда твердой фазы в результате появления на ней потенциалобразующих ионов;

образования ионной атмосферы вокруг твердой фазы;

замена ионов, образующих ионную атмосферу, ионами, находящимися в растворе (ионами того же знака).

Механизм появления потенциалобразующих ионов на поверхности твердой фазы может быть двояким:

а) полярные молекулы, образующие твердую фазу, адсорбируют из раствора ионы одного знака. Например, так же как в воде молекулы NH₃ координируют около себя ион Н⁺, образуя комплексный ион NH⁺₄

NH₃+H⁺NH₄⁺

б) Наличие потенциалобразующих ионов может оказаться следствием диссоциации полярных молекул, находящихся на поверхности тв. фазы под действием молекул воды. (процесс, аналогичный диссоциации в воде электролитов). При этом диссоциировавшие в раствор ионы образуют ионную атмосферу, а тв. фаза приобретает противоположный заряд.

Возникновение потенциалобразующих ионов и ионной атмосферы свойственно в разной степени многим твердым телам; у ионитов это свойство развито особенно сильно.

Сам же процесс ионного обмена пока не рассматривался. И начинается этот процесс в том случае, если такой ионит поместить в раствор электролита, содержащий ион, одноименный с ионом ионной атмосферы. И заключается процесс ионного обмена как раз в обмене ионов между ионной атмосферой и раствора электролита.

Например, в ионите диффузный слой (ионная атмосфера) состоит из ионов Н⁺ (ионит записывается в виде RH), и образуется при диссоциации молекулы RH по реакции:

RH R^-/H⁺.

Если такой ионит поместить в раствор NaCl, то ионы Na⁺ начнут поступать в ионную атмосферу, а из нее в раствор будут выходить ионы Н⁺ в эквивалентном количестве.

Наступившее равновесие характеризуется уравнением:

R^-/H⁺+Na⁺_р-рR^-/Na⁺+H⁺_р-р.

Иониты, применяемые для адсорбции катионов (Na⁺, Ca²⁺, Mg²⁺ и др.) носят название катионитов. Потенциалобразующий слой таких ионитов составляют анионы, а ионную атмосферу — катионы. Ионыты, применяемые для адсорбции из раствора анионов называются анионитами (потенциалобразующий слой — катионы, ионная атмосфера — анионы). Например

R⁺/Cl^-+NO₃^-R⁺/NO₃^-+Cl^-_р-р.

Характеристика ионитов и методов их получения. Минеральные иониты. История развития ионитов и ионного обмена Аристотель IV в до н.э. во время похода Александра Македонского стал пропускать через ящики с песком морскую воду. Получал опресненную воду для питья солдатам.

ХIII век н.э. Бекон повторил опыты Аристотеля Середина XIX века, Англия. Начинают применять хим. удобрения. Томас и Вей обнаружили, что в почве происходит обмен иона NH₄⁺ на ион Ca²⁺. В 1876 г. Лемберг показал, что из всех элементов почвы на обмен способны лишь такие соединения, как цеолиты и глинистые минералы (бентонитовые глины).

Начало XX века — бурное развитие техники (и энергетики). Немец Ганс в 1905 г. патентует способ искусственного приготовления минеральных катионитов (из прировдных цеолитов). Эти синтетические мин. катиониты получили название «пермутит».

К цеолитам относятся такие соединения как Анальцин Na (SrAlO₆)H₂O.

Шабазит Na₂(Sr₂AlO₆)6H₂О Это цеолиты. К глинистым минералам — соединения:

AL₂O₃4SrO₂H₂O.

AL₂O₃2SrO2H₂O.

Механизм работы таких минеральных ионитов таков: ионная атмосфера состоит или из Н⁺ или из ОН^- в зависимости от рН раствора. Кислотный или основной характер диссоциации в зависимости от рН среды и соответственно работают как катиониты в щелочной среде, и как аниониты — в кислой.

Подавляющее большинство искусственных минеральных катионитов полученных на основе алюмосиликатов в кислой среде подвергаются разложению (выделяется Н₂SiO₃). Другим недостатком таких ионитов является их малая обменная емкость и механическая прочность. Указанные недостатки являются причиной того, что в крупной энергетике минеральные катиониты практически полностью вытесненными органическими катионитами.

Органические иониты В 1935 году начался синтез органических ионитов. Открытие их принадлежит Адамсу и Холмсу, которые изучая бой грамофонных пластинок, сделанных из бекелитовой смолы, совершенно случайно обнаружили, что эти кусочки могут быть катионитом. Бекелитовая смола для пластинок получалась поликонденсацией фенола с формальдегидом:

Группой, способной к диссоциации, была фенольная группа — ОН, которая в щелочной среде (рН7) диссоциировала по типу ROHRO^-+H⁺.

Основными преимуществами органических ионитов были:

Высокая механическая прочность.

Практическая нерастворимость в воде Высокая обменная емкость.

Получились такие органические иониты путем проведения реакций полимеризации, сополимеризации, поликонденсации и сополиконденсации.

Важной задачей создания органических ионитов было (и является) введение в состав полимолекул ионита функциональных групп, т. е. групп, способных к диссоциации в воде или к адсорбции из воды ионов и созданию таким образом потенциалобразующего слоя и ионной атмосферы. Основное отличие катионитов от анионитов заключается как раз в том, что они имеют принципиально разные функциональные группы.

Функциональные группы катионитов Функциональными группами органических катионитов (т.е. группами, обладающими свойствами кислотной диссоциации) являются:

• а) карбоксильная группа — СООН (как правило слабокислотная)
• б) сульфогруппа — SO₃H (сильнокислотная).

В соответствии с наличием этих групп катиониты делятся на карбоксилатные и сульфокатиониты.

в) наряду с указанными группами во многих органических катионитах находится гидроксильная группа — ОН (в составе фенольного кольца; часто называют фенольная группа — ОН). Эта группа является очень слабокислотной, т. е. диссоциирует лишь при высоких значениях рН (рН7), что в практике водоподготовки на ТЭС, практически не бывает. Поэтому эта группа в процессе ионного обмена участвует очень слабо.

Лекция № 8

Уравнение адсорбции Гиббса выведено при таких условиях:

а) замкнутая система, в которой объем Т=const; V_i=const и имеет вид.

d=-d_iГ_i. (1).

То есть, изменение поверхностного натяжения адсорбента определяется изменением химического потенциала и изменением числа молей при переходе адсорбата из объема к поверхности.

Если концентрации всех компонентов, кроме i-го, в поверхностном слое не изменяются, т. е. d₁=d₂=…=0, но d_i0, то при Т=const и V=const уравнение примет вид:

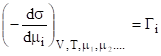
. (2).

То есть величина адсорбции i-го компонента на поверхности жидкости (адсорбента), характеризуются величиной Г_i, равна уменьшению поверхностного натяжения на единичное изменение химического потенциала i-го компонента в процессе адсорбции.

Уравнение адсорбции Гиббса — (1) и (2) — позволяет определить адсорбцию на поверхности жидкости нерастворяющегося в ней газа и адсорбцию в поверхностном слое жидкости растворенного в ней вещества; т. е. относится к системам, состоящим из двух фаз (газ-жидкость) и двух компонентов (газ-жидкость, или растворитель и растворенное вещество).

В практических расчетах уравнение адсорбции Гиббса обычно используется в ином виде. Для того, чтобы получить такое уравнение, подставим выражение химического потенциала =₀+RTlnp, справедливое для идеального газа или пара, в уравнение (2). Тогда получим:

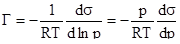
(3).

.

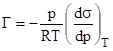
Величина Г представляет собой избыток адсорбата (газа) на поверхностном слое адсорбента (жидкости).

Для системы, представляющей собой раствор вещества в жидкости, при достаточном разбавлении раствора, химический потенциал растворенного вещества можно выразить в виде:

=₀+Rtlna или ₀+RtlnС.

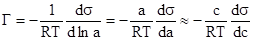
где, а и С — активность и концентрация растворенного вещества. Тогда, подставляя эти выражения в уравнение (2) получим.

.

Уравнения (3) и (4) называются уравнениями изотермы адсорбции Гиббса, и позволяют графически представить изотерму адсорбции в виде зависимости Г=f©.

Из уравнения (4) видно, что если с ростом концентрации растворенного вещества в растворе — уменьшается, т. е., если d/dc0, то Г0 и концентрация растворенного вещества в поверхностном слое больше, чем в объеме раствора, т. е. имеет место положительная адсорбция. В противном случае, т. е. если d/dc0, то Г0, и концентрация растворенного вещества в поверхностном слое меньше, чем в объеме раствора (отрицательная адсорбция).

Для водных растворов, с которыми приходится иметь дело в энергетике, веществами с положительной адсорбцией обычно являются высокомолекулярные органические вещества, называемые ПАВ. Которые используются для удаления остатков масла и мазута в отработавших водах, путем создания пены, на которой адсорбируется капельки масла (флотация).

Молекулы таких ПАВ (и других веществ с положительной адсорбцией) в поверхностном слое ориентируются, создавая как бы «частокол», в котором полярные группы, например СООН, обращены к воде, а неполярные — углеводородные радикалы — к воздуху.

Отрицательная адсорбция (Г0) в практике имеет место при растворении в воде сильных электролитов (например, солей). В этом случае ионы, на которые диссоциирует сильные электролиты взаимодействуют с молекулами воды более интенсивно, чем молекулы воды друг с другом.

Поэтому ионы преимущественно распределяются в глубине раствора и в поверхностном слое их концентрация меньше, чем в объеме.

Изотермы адсорбции газов и паров (Изотермы адсорбции Генри и Ленгмюра)

Изотермой адсорбции называется кривая, выражающая зависимость адсорбции от концентрации или от давления. Г=f© или Г=f (p).

Изотерма адсорбции является одной из важнейших характеристик адсорбционных процессов.

Простейшим уравнением изотермы адсорбции для однородной поверхности, является уравнение Генри.

Но прежде чем перейти к выводу уравнения Генри, определим понятие адсорбционного равновесия.

Адсорбционным равновесием называется состояние подвижного термодинамического равновесия обратимого процесса адсорбции, т. е. равновесие характеризуется равенством скоростей адсорбции и десорбции V_ад=V_дес.

Подобно тому, как изменяется концентрация реагирующих веществ в обратимых реакциях, в первый момент контакта адсорбента и адсорбата адсорбция вещества на поверхности идет очень быстро, а затем, по мере насыщения поверхности скорость адсорбции падает, а скорость десорбции (отрыва молекул адсорбата с поверхности) возрастает. В момент наступления равновесия V_ад=V_дес.

Уравнение изотермы адсорбции Генри выведено для адсорбентов с однородной поверхностью, к которым можно отнести сажу, стекло, слюду, монокристаллы.

При этом предполагается, что при адсорбции газов на поверхности образуется мономолекулярный слой, толщина которого зависит от размера молекул газа и их ориентации у поверхности.

Концентрация вещества в адсорбционном слое принимается везде одинаковой. Адсорбционной поверхностью может быть и жидкость и твердое вещество. В состоянии адсорбционного равновесия для каждой температуры справедливо выражение:

N мол. (в газе) n мол. (на адсорбенте) Обозначим С_а (моль/дм³) — концентрация вещества в адсорбционном слое; _а — коэффициент активности вещества в адсорбционном слое; С (моль/дм³) — концентрация вещества в газе; - коэффициент активности вещества в газе.

Тогда из закона распределения следует:

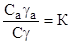
или.

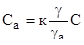
(5).

где К — константа равновесия, независящая от концентрации, или константа Генри (к=const при Т=const).

Это уравнение, представляющее собой зависимость С_а=f (C)_T есть уравнение изотермы адсорбции. При малой концентрации газа (вещества в газе) 1 и _а1, тогда С_а=кС (6).

Для идеальных газов из уравнения Менделеева-Клапейрона РV=nRT получим n/V=P/RT, т.к. n/V=C, то С=Р/RT, тогда. Подставляя © в уравнение (6), получим:

С_а=Р/RTК (7).

С_а=К/RTp (7).

Согласно уравнению 7 при малых давлениях газа, концентрация вещества со стороны газа в адсорбционном слое пропорциональна концентрации или давлению вещества в газовой фазе.

(т.е. здесь речь идет об адсорбции газа на твердой или жидкой поверхности; и под «веществом» понимается сорбат — газ).

Изотерма адсорбции Генри выглядит так:

При малых давлениях р (до р₁) с_а=f (p) носит линейный характер. При увеличении рр₁ наблюдается отклонение от линейности (кривая 2), что определяется взаимодействием адсорбирующихся молекул вещества друг с другом. Т. е. скорость адсорбции уменьшается, а при дальнейшем росте р (или концентрации газа над поверхностью) наступает адсорбционное насыщение (кривая 2 стремится к пределу).

При этом при любом давлении газа р кривая адсорбции характеризует адсорбционное равновесие, т. е. равновесие между адсорбцией и десорбцией вещества на поверхности адсорбента.

Уравнение изотермы адсорбции Ленгмюра Это уравнение также относится к случаю адсорбции газа (пара) на жидком или твердом адсорбенте. Это уравнение более точное, чем уравнение Генри. Выведено оно при таких предположениях:

Число мест на поверхности адсорбента ограничено, поэтому с_а увеличивается до С_а^max, т. е. до насыщения.

Связь молекул вещества с адсорбентом достаточно прочна и адсорбированные молекулы не перемещаются по поверхности.

Адсорбция на одном месте не влияет на состояние другого.

Между адсорбированными молекулами отсутствует взаимодействие.

При равновесии скорость адсорбции равна скорости десорбции.

Скорость адсорбции пропорциональна концентрации (давлению) газа и количеству «свободных мест» поверхности адсорбента., т. е.

V_адс=к₁С (1-).

Где — доля занятых мест,.

(1-) — доля свободных мест на поверхности:

к₁ — константа скорости адсорбции.

Молекула десорбируется, если ее энергия достаточна для отрыва от поверхности. Число таких молекул пропорционально общему числу адсорбированных молекул: тогда v_дес=к₂

Где к₂ — постоянная величина (константа скорости десорбции).

В момент равновесия: к₁С (1-)=к₂ откуда к₁С₁-к₁С=к₂ и = к₁С/(к₂+к₁С), делим числитель и знаменатель на к₂ тогда.

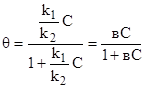
, (8).

где к₁/к₂=в — постоянная для данного адсорбента (или коэффициент адсорбции).

Величина адсорбции вещества (газа) на поверхности Г выражается уравнением Г=Г_max, т. е. пропорциональна максимально возможной адсорбции (Г_max) при всей занятой поверхности доля занятых ан поверхности мест .

Т.е. при =1 вся поверхность адсорбента покрыта мономолекулярным слоем адсорбированных молекул — Г=Г_max.

Подставляя из уравнения (8), получим.

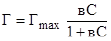
. (9).

Это уравнение носит названия изотермы адсорбции Ленгмюра. Графически изотерму адсорбции Ленгмюра можно показать, т. е. зависимость Г=f© или Г=f (p). При малых значениях С, т. е. при малых давлениях газа над поверхностью вс1 и уравнение адсорбции Ленгмюра принимает вид Г=Г_maxвС, т. е. уравнение имеет вид Г=кС — а это не что иное, как уравнение Генри, т. е. при малых давлениях газа уравнение Ленгмюра переходит в уравнение Генри (участок I). При больших давлениях газа (большие значения С) вС1 и уравнение Ленгмюра принимает вид: Г=Г_max..

То есть адсорбция в насыщенном состоянии не изменяется с изменением р (или С) — этому соответствует участок III графика. Участок II — переход от линейной адсорбции к насыщению. Уравнение адсорбции Ленгмюра достаточно хорошо согласуется с опытными данными в области I и III, и не достаточно хорошо в области II. Это связано с тем. что при выводе сделан ряд допущений, тогда как на самом деле:

• а) поверхность адсорбента неоднородна;
• б) между адсорбированными частицами имеет место взаимодействие;
• с) в ряде случаев встречается не моноа полимолекулярная адсорбция.

Учет неоднородности поверхности адсорбента (особенно в твердых фазах) позволили Фрейндлиху получить такую эмпирическую зависимость Г=КС^1/n где К и n — постоянные величины. Учет взаимодействия молекул вещества, адсорбированных на поверхности провели Брунауэр, Эммит и Теллер. В результате они получили формулу.

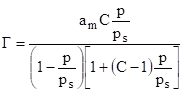
(10).

где Г — количество адсорбируемого вещества; а_m — емкость одного монослоя; р_s — давление насыщенного пара над поверхностью адсорбции; С — некоторая постоянная; Р — давление газа.

Это уравнение получило название уравнение адсорбции БЭТ по имени трех авторов.

Зависимость адсорбции от температуры и вида газа

В уравнении Ленгмюра коэффициент адсорбции в=к₁/к₂. (к₁ — константа адсорбции; к₂ константа десорбции). Так вот, величина к₁ мало зависит от температуры. Константа к₂ зависит от температуры. Для того, чтобы адсорбированная молекула могла покинуть поверхность адсорбента, она должна обладать энергией, большей теплоты адсорбции (энергии адсорбционных сил). Повышение температуры увеличивает кинетическую энергию молекул и облегчает десорбцию. Зависимость к₂ от температуры подчиняется закону Больцмана:

к₂=к₀е^-Q/RT

где Q — теплота адсорбции. Таким образом, с увеличением температуры количество газа, адсорбированного на поверхности уменьшается. Что касается зависимости адсорбции от вида газа, то при малых давлениях газа существенных различий в адсорбции нет, а при больших давлениях газа над поверхностью адсорбента сильнее адсорбируются те газы, которые легче конденсируются в жидкость, и которые, следовательно, обладают высокой температурой кипения.