Матричные игры. 
Теория игр

В результате освоения данной главы студент должен:

знать

• • определения понятий «игра с нулевой суммой», «антагонистическая игра», «матричная игра», «седловая точка», «цена игры», «чистая стратегия», «смешанная стратегия», «решение матричной игры» ;
• • основные свойства матричных игр;
• • основные факты о содержательной взаимосвязи между теорией матричных игр и теорией линейного программирования;

уметь

• • находить решение матричной игры путем сведения ее к паре взаимно двойственных задач линейного программирования;
• • находить решения матричных игр, допускающих применение графического метода;

владеть

• • терминологическим аппаратом, применяемым при построении и последующем анализе матричных игр;
• • базовыми навыками применения матричных игр при моделировании ситуаций, связанных с принятием решений в условиях антагонистических конфликтов.

Среди некооперативных игр принято выделять важный класс, получивший название игр с нулевой суммой.

Игру называют игрой с постоянной суммой (с нулевой суммой), если в ней сумма значений функций полезности игроков в любых ситуациях постоянна (равна нулю):

(1.1).

Равенства значения const нулю всегда можно добиться за счет преобразования функций 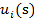в функции 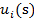= 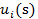- const. Как известно, данная операция не меняет оптимизационных свойств функциональных зависимостей, а следовательно, не повлияет па выбор игроками тех стратегий, которые они считают наилучшими.

Нетрудно догадаться, что в играх с нулевой суммой увеличение полезности у одних игроков означает уменьшение ее у других. Образно говоря, для того чтобы один что-то нашел, другой должен это потерять.

Игры с нулевой суммой и двумя участниками называют антагонистическими.

Название отражает то обстоятельство, что в таких играх распределение ролей «нашедший — потерявший» очевидно.

Антагонистические игры с конечными множествами стратегий у участников называют матричными.

Такое наименование связано с тем, что игры данного класса могут быть однозначно заданы с помощью матриц размерности m? n в которых количество строк m определяется числом стратегий игрока 1, а количество столбцов n — числом стратегий игрока 2.

Ситуации в матричной игре однозначно определяются парами (i, j), что означает — 1-й игрок (игрок 1) применил свою i-ю стратегию (из множества допустимых стратегий {1, 2, i,…, n}), а его оппонент (игрок 2) — его j-ю стратегию из множества {1, 2,…, i,., n).

Обозначим матрицу игры как.

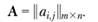
Ее элементы С1у задают значения полезностей (выигрышей, платежей) игрока 1 в ситуации (i, j). Соответственно, полезности (выигрыши, платежи) игрока 2 в этой ситуации будут равны ().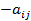

Классическим примером матричной игры является игра «четное-нечетное». В ней имеется два участника, которые одновременно и независимо друг от друга загадывают два натуральных числа. Если сумма чисел оказывается четной — выигрывает первый, в противном случае — второй. Очевидно, что каждый из игроков имеет, но существу две стратегии: загадать четное число либо загадать нечетное. Матрица игры представлена в табл. 1.1. Выигрышу в ней (игрока 1) соответствует (+1), проигрышу (-1). Строки в таблице соответствуют стратегиям игрока 1, столбцы — стратегиям игрока 2.

Аналогичным образом может быть построена матрица для другой широко известной игры — «камень, ножницы, бумага» (табл. 1.2). В ней каждый из двух игроков имеет три стратегии: выбрать камень, ножницы или бумагу. Согласно правилам (камень побеждает ножницы, ножницы — бумагу, бумага — камень) определяются выигрыши, проигрыши либо ничья (при совпадении комбинаций).

Таблица 1.1

Матрица игры «четное-нечетное» .

Таблица 1.2

Матрица игры «камень, ножницы, бумага» .

В качестве тренировочного примера старательному читателю может быть предложено самостоятельно построить матрицу для расширенного варианта данной игры, известного по сериалу «Теория Большого взрыва» («The Big Bang Theory»). Там один из героев (Шэлдон Купер) предлагает игру «камень, ножницы, бумага, ящерица, Спок» .