Детерминизм в тепловых процессах природы

Человек может сделать путь великим, нс путь делает великим человека.

Конфуций

История открытия закона сохранения и превращения энергии привела к изучению тепловых явлений в двух направлениях: термодинамическом изучающем тепловые процессы без учета молекулярного строения вещества, и молекулярно-кинетическом, исследующем тепловые явления ка результат совместного действия огромной совокупности движущихс частиц, из которых состоит вещество. Термодинамика возникла из обобщения многочисленных фактов, описывающих явления передачи, распространения и превращения тепла. Молекулярно-кинетическое направлени характеризуется рассмотрением различных макропроявлений систем ка результата суммарного действия огромной совокупности хаотически движущихся молекул. При этом молекулярно-кинетическая теория использует статистический метод, интересуясь не движением отдельных молекул, а только средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название — статистическа физика. Оформившись к середине XX в., оба эти направления подходя к рассмотрению изучения состояния вещества с различных точек зрени и дополняют друг друга, образуя одно целое.

На основе исследований Джоуля, Майера и других ученых установлено так называемое первое начало термодинамики. Клаузиус первым высказал мысль об эквивалентности работы и количества теплоты как о перво начале термодинамики. Всякое тело имеет внутреннюю энергию, котору Клаузиус назвал «теплом, содержащимся в теле» (II) в отличие от «тепла сообщенному телу» ((2). Величину V можно увеличить двумя эквивалентными способами, произведя над телом механическую работу (А) или сообщая ему количество теплоты (0.

Общепризнанным является тот факт, что распространение тепла представляет собой необратимый процесс и тепло передается от горячего тела к холодному, а не наоборот. Важной концепцией термодинамики является то, что при работе тепловой машины не все количество теплоты, взято у нагревателя, передается холодильнику (рис. 10.1). Часть этой теплот превращается в работу, совершаемую машиной. Клаузиус показал, чт объяснение превращения теплоты в работу основывается еще на одно принципе, сформированном С. Карно, утверждающем, что в любом непрерывном процессе превращения теплоты от горячего нагревателя в работ непременно должна происходить отдача теплоты холодильнику. Совершаемая при этом тепловая работа (Л) оценивается коэффициентом полезног действия (г|) следующим образом: г| = Л/(21, где — количество теплоты переданное нагревателем. Максимальный коэффициент полезного действия имеет идеальная тепловая машина, работающая по циклу Карно коэффициент полезного действия которой определяется как ц = (Т_{— Т₂)/Т₂ где Т_х — абсолютная температура нагревателя, Т₂ — абсолютная температура холодильника.

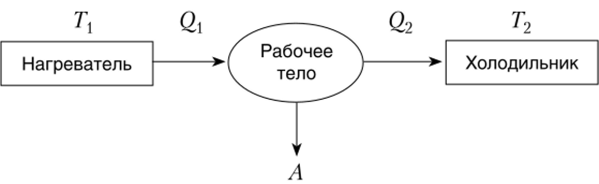
Рис. 10.1. Схема тепловой машины

Таким образом, имеет место общее свойство теплоты, заключающееся в том, что теплота «всегда обнаруживает тенденцию к уравниванию температурной разницы путем перехода от теплых тел к холодным». Эт положение Клаузиус предлагает назвать «вторым основным положение механической теории теплоты» и в современную науку вошло как второ начало термодинамики.

Все эти многочисленные факты и нашли свое обобщение и теоретическое объяснение в законах классической термодинамики:

• 1) если к системе подводить тепло (2 и над ней производится работа Л то энергия системы возрастает до величины /7: и = (2 + Л. Эту энергию /7 В называют внутренней энергией системы;
• 2) невозможно осуществить процесс, единственным результатом которого было бы превращение тепла в работу при постоянной температуре, г. е тепло не может перетечь самопроизвольно от холодного тела к горячему.

В первом законе речь идет о сохранении энергии, а во втором — о невозможности производства работы исключительно за счет изъятия тепла из одного резервуара при постоянной температуре, т. е. о направлени тепловых процессов в природе.

Благодаря работам австрийского физика Людвига Больцмана термодинамика была сведена с макроскопического уровня на микроскопический. Состояние макроскопического тела (системы), заданное с помощью макропараметров (параметров, которые могут быть измерены макропри борами, — давление, температура, объем и другие макроскопические величины, характеризующие систему в целом), называют макросостоянием. Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием. Всякое макросостояние может быт осуществлено различными способами, каждому из которых соответствуе некоторое микросостояние системы. Число возможных различных микросостояний, соответствующих данному макросостоянию, называют термодинамической вероятностью (?) макросостояния.