Статистическое оценивание параметров

8.1. Точечные оценки неизвестных параметров распределения

Пусть у нас имеется выборка (x_lt х₂,…, х_п) из ГС, распределение которой зависит от неизвестного параметра 0.

Определение 8.1. Точечной оценкой параметра 0 называется статистика 0″ =0(х₁,…, х"), значение которой, при заданной реализации выборки, принимают за приближенное значение параметра 0.

Ясно, что для оценивания 0 можно использовать различные оценки, и чтобы выбрать лучшую из них, надо иметь критерии сравнения качества оценок.

А Определение 8.2. Оценка 0″ неизвестного параметра 0 называется несмещенной, если М0″ =0.

А Определение 8.3. Оценка 0″ неизвестного параметра 0 называется состоятельной, если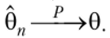

А Определение 8.4. Оценка 0* неизвестного параметра 0 называется эффективной, если она оптимальна в среднеквадратическом смысле, т. е. имеет минимальное 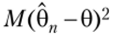среди всех возможных оценок параметра 0.

(т.е. если 0 — любая другая оценка, то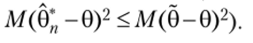

Если эффективная оценка ищетсясреди несмещенных оценок, то, так как М0_И =0, имеем 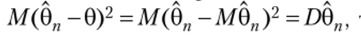г. е. эффективная оценка — оценка с наименьшей дисперсией.

Ранее мы говорили, что выборочные характеристики используются в качестве оценок теоретических характеристик. Выясним, насколько хороши эти оценки, исходя из критериев, которые мы определили выше.

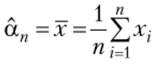
Пусть х_п — выборка из ГС с неизвестными математическим ожиданием, а и дисперсией ст². В качестве оценки, а возьмем Так как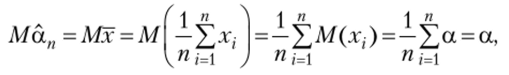

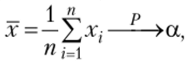
то х — несмещенная оценка. Так как x_v …, х_п — независимые, одинаково распределенные СВ с конечным математическим ожиданием а, то по следствию из закона больших чисел в форме Чебышева т. е.

х — состоятельная оценка.

Вопрос об эффективности оценки решается при наличии дополнительной информации — знания закона распределения ГС. Если ГС имеет нормальное распределение, то х — эффективная оценка. Если же ГС имеет равномерное распределение, то оценка х не является эффективной. Например, можно взять величинукоторая будет более эффективной.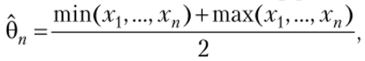

В качестве оценки о² возьмем выборочную дисперсию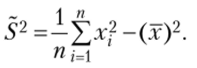

Выясним вопрос о несмещенности данной оценки, для чего подсчитаем ее математическое ожидание:

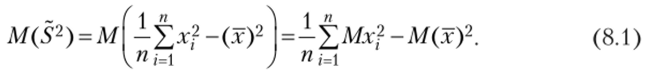
Так как 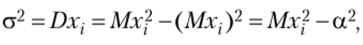то.

С одной стороны,.

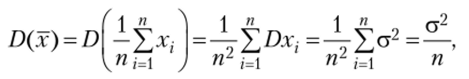
с другой — 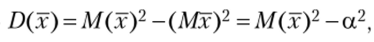откуда.

Подставляя выражения (8.2) и (8.3) в формулу (8.1), получим.

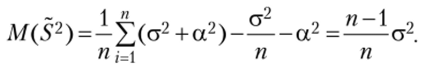
Следовательно, S² — смещенная оценка для а². Но если и можно использовать эту оценку.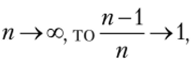

Рассмотрим новую оценку 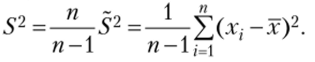Очевидно, что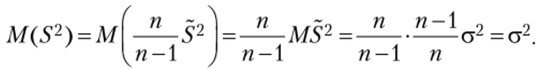

Следовательно, S² — несмещенная оценка.

Выясним состоятельность S² как оценки. Рассмотрим последовательность СВ 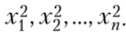Эти СВ независимы, одинаково распределены и.

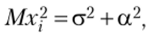т. е. имеют конечные математические ожидания. По следствию из закона больших чисел в форме Чебышева 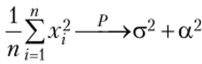. Мы уже показывали, что 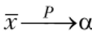., значит, по свойствам сходимости по вероятпости 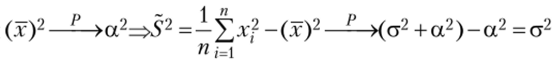, т. е. S² — состоятельная оценка для а².

Так как 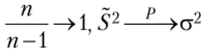, то по свойствам сходимости по вероятности.

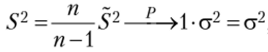, т. е. S² — также состоятельная оценка.

Очевидно, что ЭФР F_n(x) можно рассматривать как оценку теоретической ФР F^(x) ГС, из которой извлечена выборка х_п). Выясним качество этой оценки. Рассмотрим испытания Бернулли, связанные с нашей выборкой, и за успех примем событие У = {x_t <�х}. Тогда Р (У) = Р{х₁ Обозначим через ц (х) число успехов в испытаниях Бернулли, тогда.

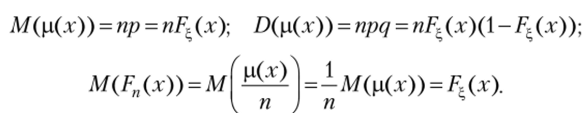
Таким образом, F_n(x) — несмещенная оценка F^(x).

По закону больших чисел в форме Бернулли 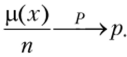Следовательно,.

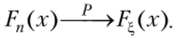Таким образом, F_n(x) — состоятельная оценка для F^(x).