Связи распределений. 
Теория вероятностей

Установление связей между распределениями имеет большое теоретическое и практическое, конструктивное значение при изучении и моделировании распределений. Этот аспект обычно упоминается в курсах теории вероятности вскользь. В данном параграфе делается попытка систематического изложения вопроса в форме установления интересующих нас связей между конкретными распределениями. Изложение материала проводится в форме отдельных утверждений с доказательствами (кроме тех, которые доказаны ранее в основном курсе вероятности).

Утверждение 4.1. Из независимости СВ X, — В ( 1, р) => СВ.

П

Х= X X, ~ В{п, р) (доказано в гл. 2).

1−1.

Утверждение 4.2. Пусть независимые СВ X, ~ G (p); У, — сдС (/?); Z, — IIa (r, р), Z₂ ~ ОВ (г, р). Тогда верны равенства Х_: = Y-, + 1; Z, = Z₂ + г;

Z, = X X; Z₂ = X У, (доказано в гл. 2).

i=i i-i.

Утверждение 4.3. СВ X ~ H (N, М, п); СВ У ~ В (п, р); условия асимптотики:

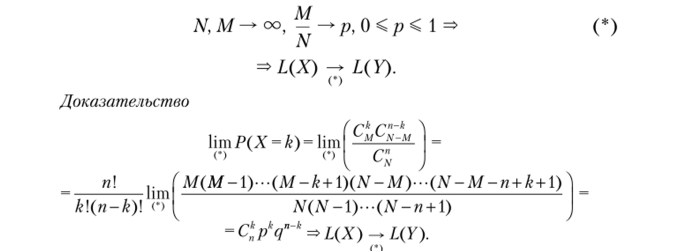
Утверждение 4.4. СВ X ~ В (п, р), СВ У — П (А.). Условия асимптотики:

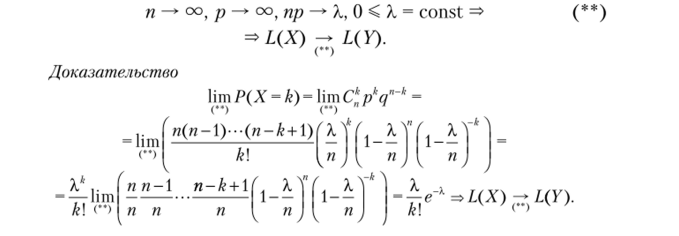
Утверждение 4.5. Пусть г неразличимых шаров размещают по п ящикам без ограничений па число шаров в ящике. Условия асимптотики:

Утверждение 4.6. Из N элементов, среди которых М первого типа, производится выборка без возвращения до появления в выборке впервые элемента первого типа; X — число выбранных элементов;

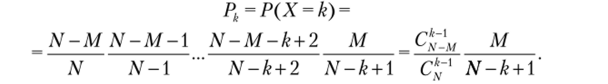
Условия асимптотики:

Замечание 4.10. Аналогично доказывается, что если выборка производится до появления в выборке г элементов первого тина в условиях асимптотики (****) и СВ Z, — число выбранных элементов, Z, — число элементов второго типа среди выбранных, a Y = Z₂ при r= 1, то имеем: L (Y)^* сдС (У); /.(Z,) IIa (r, р); L{Z>) ОВ (г, р).

Утверждение 4.7. СВ Х₀ — /?|0; 11; СВ X — Ra; b[, тогда СВ X = = Х₀(Ь - а) + а (доказано в гл. 2).

Утверждение 4.8. СВ Х₀ ~ А'(0, 1); СВ X ~ N (a, а); тогда СВ X = = стХО + а (доказано в гл. 2).

Утверждение 4.9. СВ X — Е (к); Y — Г_цД => Е (X) = Г_а__1Д (доказано в гл. 2).

Утвеождение 4.10. Пусть СВ X — В (п. и. Y ~ Р_п(п. тт-,…т_к

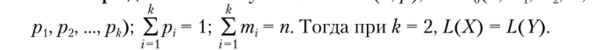
Доказательство. Очевидно, что при k = 2, р, = р, т_{ + т, = п из вида ЦУ).

к я Утверждение 4.11. СВ Y ~ R — — угол вращения луча вокруг точки с координатами (0; 1); СВ X — точка пересечения этого луча с осью Ох (рис. 4.16). Тогда СВ X имеет распределение Коши.

с плотностью распределения /_х(х) =-s- (доказано в гл. 2).

тс (1 + эс)

Рис. 4.16. К утверждению 4.11 Утверждение 4.12.

— плотность распределения Стыодента. СВ Y ~ Коши — /Дх) = 1.

=-=-. Тогда при k = имеемL (X) = L (Y) (доказано в парагра;

7 г (1 + X)

фе 4.3).

Утверждение 4.13. СВ X- N (0, а,), СВ Y~ N(0, о_у), Хи У — не;

У зависимы, а_л = ст_(/ = а. Тогда СВ Z—распределена по закону Ко;

X.

ши с плотностью распределения g (х) =-5-.

я (1 + х)

Доказательство

G_z(z) = jjf (^x, y) dxdy = ^<2j' ^ ~ ^заштР^{ихованная} область на рис. 4.17.

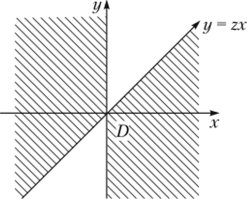
Рис. 4.17. К утверждению 4.13.

Рассмотрим следующие случаи: у

а) х > 0, тогда — < z, y < xz;

х

У

б) х < 0, тогда — > z, у > xz.

х

О +СО +оо ZX

Тогда С_г(г)= J dx J f (xy)dy + J dx j f (x, y) dy.

zx 0.

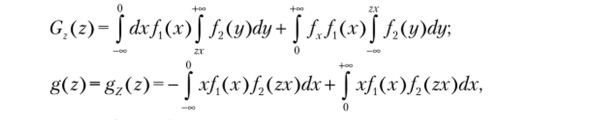
Если X и У независимы, то тогда при X, У — МО, ст = 1).

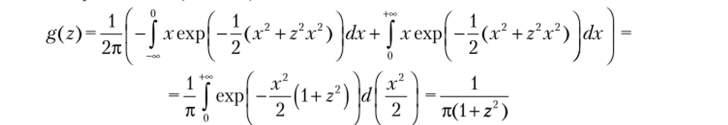
— а это плотность распределения закона Коши.

Y <�т,.У, X Y

При а,. = а" = а ^ 1 имеем Z —-, где X, = —; У, = —; = a_Yl

— У ст_хХ, а_х ay.

= 1 =>g (z) =

л (1 + г)

Утверждение 4.14. СВ Xимеет бета-распределение с плотностью 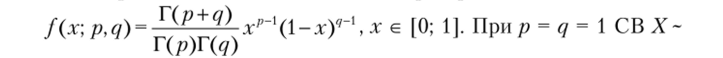- В (1, 1) имеет распределение Щ 0; 11.

Доказательство. Пусть р = q = 1, тогда.

а это плотность распределения СВ X ~ /?[0; 11.

Утверждение 4.15. СВ X ~ В (п, р), npq > 9. Тогда.

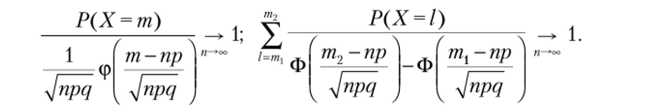
Доказательство. Первое утвеждение следует из ЛТМЛ, а второе — из ИТМЛ.

Утверждение 4.16. СВХ~ R[0; ]X (k) — k-я порядковая статистика; f_k(x) — ее плотность распределения (Х (к) — k-e наблюдение над СВ X по возрастанию). Тогда L (X (k)) = B (k, п - k + 1).

Доказательство. f (x) = 1, F (.v) =х при х е [0; 1].

В математической статистике будет получено распределение СВ X (k) в виде.

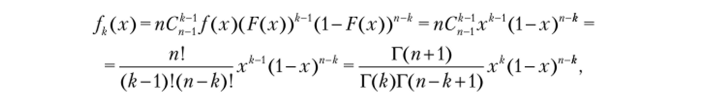
а это плотность бета-распределения с р = к: q = п — k + 1 (так как р + q = = п + 1) с плотностью распределения вида.

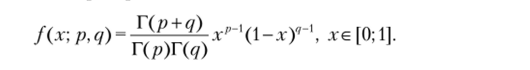
Утверждение 4.17. Пусть СВ Y ~ N (0, 1). Тогда СВ Z = Y² ~ %²_V

т.е. имеет распределение хи-квадрат с параметром (числом степеней свободы), равным 1, и в то же время Z — r,_{/2i ½}. Кроме того, имеется эквивалентность распредений: yj_n ~ Г"_/21/2.

Выпишем полученную в параграфе 4.3 характеристическую функцию для СВ X ~ Г_{а х}: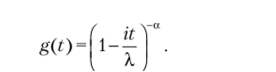

'Гогда характеристическая функция у, есть g, (I) = (1 -2it) ², а для у²"

¹ Xi ^п

п

получаем g^₂(t) = (l-2it) ², отсюда.

Утверждение 4.18. СВ Т = U J^> ^ГД^С U~N (0,1); V~ у?, -оо <�х< оо, имеет распределение Стьюдента.

Доказательство. Обозначим через G (t) функцию распределения СВ Т:

Найдем совместную плотность распределения СВ U и V:

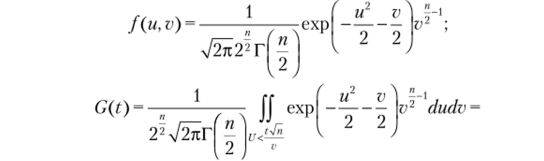
HI.

Утверждение 4.19. Пусть СВ _т — независимы, ?, = 2^²;

i=i.

п

СВ у_и г|_я — независимы, г = X г|²; г|_;~ N (0, a²); i = 1,…, т J =

• 7"1
• ?

= 1, …, п] X = —; тогда СВ X имеет распределение Фишера с нлотП ностью.

Дифференцируем F_m«(t) по t₉ получим f_mn(t) — плотность распределения Фишера.

Утверждение 4.20. Закон распределения Фишера F"," в точке.

• —— совпадает с бета-распределением с плотностью распределе-
• 1 ¹ _fл т п

ния /_р(х; р, q) при р = -, q = -.

Доказательство. Проверим это утверждение непосредственным вычислением:

Ч.Т.Д.

t

T.c.fJt; р, q) совпадает с плотностью распределения Фишера в точке-,.

1 —1

Утверждение 4.21 (связь геометрического и показательного распределений). Показательное распределение возникает как предельное для геометрического распределения G (p) в следующей схеме: в моменты времени 0, h, 2h, … (h -* 0) производятся независимые испытания с вероятностью успеха, равной Р_и = Xh (X = const > 0); X_h — момент первого успеха. Тогда число испытаний до первого успеха Y ⁼ -р ~ Г (р = Xh). h

Доказательство

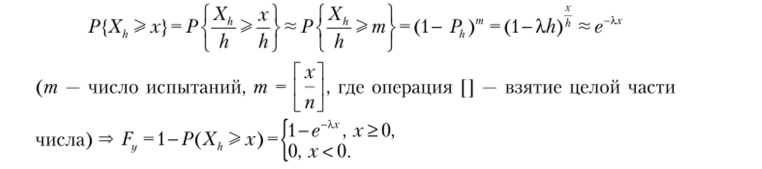
Х^ке~^х

Утверждение 4.22. Пусть ?, — Р (Х), Р (х = к) =, к = О, 1, 2,.

гС I.

тогда L (x)—yN (k, JX).

->оо

Доказательство. Имеем.

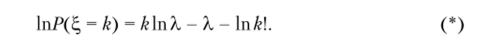
кроме того,.

_x+i (( V.

Пусть известно, что Г (?+1) = А. ²е" ^хл/2тг 1 + о; кроме того,.

I WJ.

Г(k + 1) = А'!, так как к — целое; поэтому.

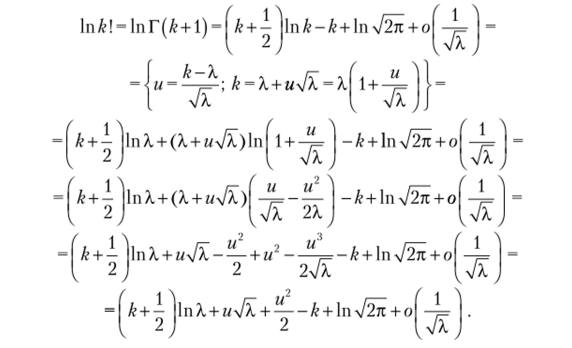
Подставив полученное выражение в формулу (*), получим 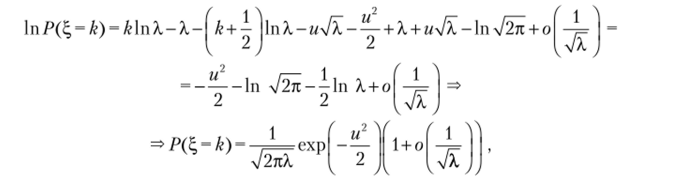что соответствует '(к, 4к), ч.т.д.

Для следующего утверждения нам понадобится определение пуассоновского потока. Пуассоновским потоком называется поток событий, таких что:

• 1) числа наступлений событий в непсресекающихся интервалах независимы (независимость приращений);
• 2) + t₀) — ?(*ь) = ^(у) — %(()) = t) (однородность, или стационарность);

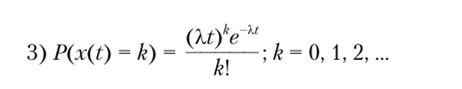
Утверждение 4.23. Связь распределений Е (Х) и n (Xt). Пусть в пуассоновском потоке ^(1) — количество событий ?, за время t.

(Xt)^he^>J

Тогда ^(f) — n (Xt), т. е. P (x (t) = k)———, а интервалы времени.

A?!

между событиями T_t ~ Е (Х).

Доказательство. Обозначим Т, — время между соседними событиями пуассоновского потока. Тогда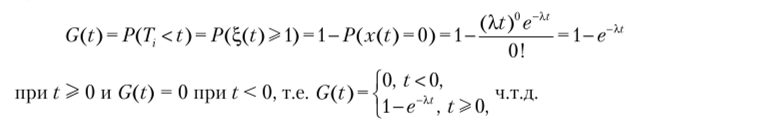

Утверждение 4.24 (связь распределений Г_аД и п (Х)). Пусть ?, ~ Г_аД, г| ~ д (Лл'). Если брать, а — натуральные числа и X =1, то при указанных частных значениях параметров, а и X в целых точках гамма-распределение совпадает с пуассоновским и является при этих значениях параметров непрерывным аналогом распределения Пуассона.