Положительно определенные квадратичные формы

При построении функции Ляпунова широко используются квадратичные формы 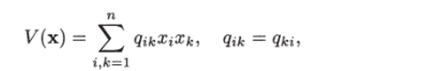или, в матричной форме,.

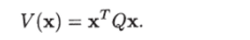
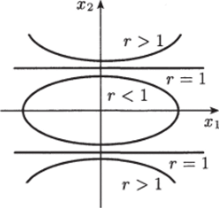
Это уравнение при г < 1 представляет собой уравнение эллипса.

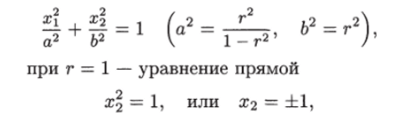
Рис. 4.1. Кривые уравнения.

/1 _ j, 2.

Таким образом, в данном случае по- ^{v; 1 2}

верхности (кривые) уровня V(х) = с являются замкнутыми только при г < 1 (рис. 4.1).

и при г > 1 — уравнение гиперболы.

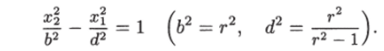
Любую квадратичную форму в матричной записи можно представить так, чтобы в ней матрица была симметрической. Поэтому всегда предполагается, что матрица, используемая при записи квадратичной формы, по определению является симметрической матрицей. Так как симметрические матрицы в методе функций Ляпунова играют важную роль, то кратко остановимся на их свойствах.

Симметрическая матрица Q называется положительно (отрицательно)I определенной матрицей, если квадратичная форма К (х) = = x^TQx является положительно (отрицательно) определенной функцией, и положительно (отрицательно) полуопределенной матрицей, если квадратичная форма У (х) = x^TQx является положительно (отрицательно) полуопределенной функцией.

Симметрическая матрица Q обладает следующими свойствами [21]:

• 1) все ее собственные значения (характеристические числа), т. е. корни А* (г = 1,2,…, п) ее характеристического уравнения det (Q — IX) = 0 являются вещественными числами;
• 2) если она положительно (отрицательно) определена, то все ее собственные значения являются положительными (отрицательными): Aj > О (Ai < 0); если она положительно (отрицательно) полуопределена, то все ее собственные значения являются неотрицательными (неположительными): А* ^ 0 (Xi ^ 0);
• 3) определитель симметрической матрицы равен произведению ее собственных значений: det Q = Л1Л2 … А_п.

Дальше часто будет использоваться одно свойство квадратичной формы. Сформулируем его в виде леммы.

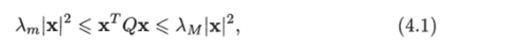
где Х_т — минимальное, а Хм — максимальное собственное значение матрицы Q.

Лемма 4.1 [7]. Квадратичная форма V (x) = x^TQx удовлетворяет неравенству

Доказательство. Для доказательства рассмотрим задачу о минимальном и максимальном значениях квадратичной формы V (x) = x^TQx на сфере |х|² = г². Согласно известным правилам определения условного экстремума составим функцию Лагранжа:

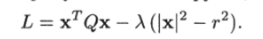
Здесь Л — неопределенный множитель Лагранжа. Представим |х|² в виде скалярного произведения векторов:

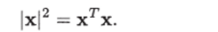
Необходимое условие экстремума принимает вид.

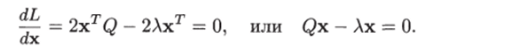
Последнее уравнение представляет собой систему однородных скалярных уравнений, и оно имеет ненулевое решение, если определитель этой системы равен нулю:

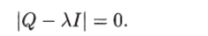
Таким образом, квадратичная форма V (x) = x^TQx принимает экстремальные значения на сфере |х|² = г², если х удовлетворяет уравнению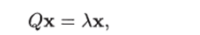

когда Л принимает собственные значения матрицы Q. Так как матрица является симметрической, то ее собственные значения являются вещественными.

Умножив последнее равенство слева на х^т, получим.

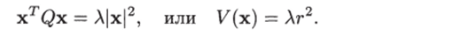
Отсюда, если А_т — минимальное собственное значение и Хм — максимальное собственное значение матрицы Q, то.

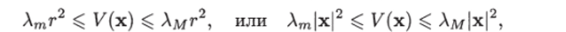
что и требовалось доказать.

Если квадратичная форма V(х) = x^TQx положительно определена, то, как следует из неравенства (4.1) и свойства положительно определенной матрицы, она неограниченно возрастает при стремлении точки х к бесконечности:

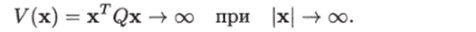
Выясним, когда квадратичная форма является положительно определенной функцией, или симметрическая матрица является положительно определенной.

Критерий Сильвестра [21 . Для того чтобы квадратичная форма V(х) = x^TQx была положительно определенной функцией, необходимо и достаточно, чтобы все определители

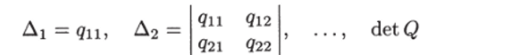
были положительны.

Пример 4.1. Дана квадратичная форма.

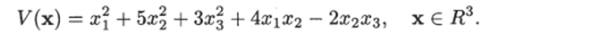
Исследовать, является ли эта форма положительно определенной функцией.

Решение. Если записать данную квадратичную форму в матричной форме, то элементами соответствующей матрицы Q будут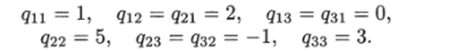

Определители.

все положительны. Следовательно, по критерию Сильвестра данная квадратичная форма является положительно определенной функцией.