Введение. 
Механика жидкости

Гидростатика — это раздел гидравлики (механики жидкости), изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределения в ней давления. Основные величины, используемые в гидростатике, — это давление p и напор H.

В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (например, плотность, вязкость, удельный вес, удельный объём). Студенту нужно уметь определять основные физические характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение и др.

гидравлика жидкость давление равновесие.

Физические свойства жидкости

Существуют следующие физические свойства жидкости:

1) Плотность — это масса единицы объёма жидкости (кг/м3):

= m/V,.

где m — масса, кг;

V — объём, м3.

Плотность воды при температуре +4С равна 1000 кг/м3. Легко заметить, что плотность воды зависит от температуры незначительно. В большинстве гидравлических расчётов свойствами сжимаемости и температурного расширения жидкостей пренебрегают, например, для воды считают плотность постоянной и равной 1000 кг/м3.

2) Удельный вес — это вес единицы объёма жидкости (Н/м3):

= G/V,.

где G — вес (сила тяжести), Н;

V — объём, м3.

Связаны удельный вес и плотность через ускорение свободного падения (g = 9,81 10 м/с2) так:

= g.

3) Коэффициент объёмного сжатия w (Па-1) — это относительное изменение объёма жидкости при изменении давления на единицу:

.

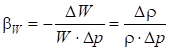
где W — изменение объёма W;

? — изменение плотности, соответствующее изменению давления на величину? p.

Величина, обратная коэффициенту объёмного сжатия, называется модулем упругости жидкостей Eж (Па):

Еж = 1/ W.

Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления? p = p — p0, а изменение объёма W=W-W0, то:

W=W0 · (1-W · ?p),.

=0 · (1-W · ?p).

4) Коэффициент температурного расширения t (0С)-1 выражает относительное изменение объёма жидкости при изменении температуры на один градус:

.

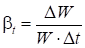
где ?W — изменение объёма W, соответствующее изменению температуры на величину? t.

Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей? t с увеличением давления уменьшается. Если принять, что приращение температуры? t = t — t0, а изменение объёма? W = W — W0, то:

W=W0 (1+t -?t),.

=0 (1+ t · ?t).

5) Вязкость — это свойство жидкости проявлять внутреннее трение при её движении, обусловленное сопротивлением взаимному сдвигу её частиц. В покоящейся жидкости вязкость не проявляется. Количественно вязкость может быть выражена в виде динамической или кинематической вязкости, которые легко переводятся одна в другую.

Вязкость динамическая ?, Па с = Н с/м2. Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и её температурой.

В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости (м2/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:

Вязкость кинематическая, м2/с.

Вязкость проявляется в том, что при движении жидкости возникает сила внутреннего трения Т между перемещающимися один относительно другого слоями с площадью соприкосновения S. определяется законом Ньютона:

.

где S — площадь соприкасающихся слоёв, м2;

du — скорость смещения слоя «b» относительно слоя «a», м/с;

dy — расстояние, на котором скорость движения слоёв изменилась на du, м;

du/dy — градиент скорости, изменение скорости по нормали к направлению движения (с-1).

Если силу трения T отнести к единице площади соприкасающихся слоёв, то получим величину касательного напряжения, которую можно определить по формуле:

.

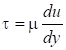
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (0Е). Градус Энглера (0Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости? применяется формула Убеллоде:

.

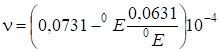
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости определяют по формуле:

? = c · Tж · 10−4,.

где с — постоянная прибора;

Tж — время истечения жидкости, с.