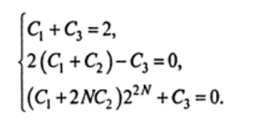Неоднородные линейные разностные уравнения

Основным методом отыскания решения неоднородного линейного разностного уравнения является следующая теорема, которую мы приводим без доказательства.

Теорема 21.1. Общее решение уравнения (21.3) является суммой его частного решения У и общего решения (21.10) соответствующего однородного уравнения (21.8):

Для нахождения общего решения неоднородного линейного разностного уравнения (21.3) разработан метод вариации постоянных, во многом аналогичный методу для дифференциальных уравнений. Однако этот метод достаточно громоздкий, и во многих случаях проще подобрать частное решение Y (i) неоднородного уравнения или «угадать* такое решение по виду правой части /(/).

Решение линейных уравнений с постоянными коэффициентами

Определение 6. Уравнение вида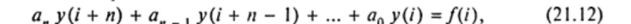

где а_п, а_п _ _м …" а₀ — действительные числа, называется разностным уравнением п-го порядка с постоянными коэффициентами относительно неизвестной функции у, определенной на некотором множестве целых чисел /.

Соответствующее однородное уравнение имеет вид:

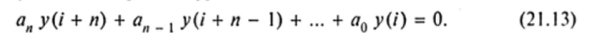
Будем искать частные решения этого уравнения в виде и (i) = q где q — число, подлежащее определению. Подставляя u (i) в уравнение (21.12) вместо у (/), получаем: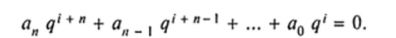

Мы ищем ненулевое решение, тогда, сокращая обе части этого уравнения на q‘> получим уравнение для q:

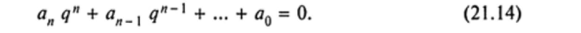
Такое уравнение называется характеристическим уравнением для однородного уравнения (21.13). Корни характеристического уравнения соответствуют линейно независимым решениям уравнения (21.13).

Рассмотрим каждый возможный случай корней характеристического уравнения.

1. Пусть уравнение (21.14) имеет п разных простых корней q_v q_v …, q_n. Тогда функции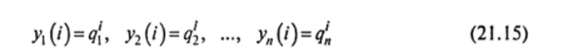

являются линейно независимыми решениями уравнения (21.13). Иными словами, общее решение уравнения (21.12) согласно свойству 2 и формуле (21.10) имеет вид:

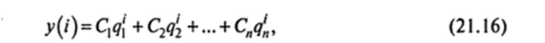
где С, С₂, С_п — произвольные постоянные.

2. Пусть среди корней характеристического уравнения (21.14) имеются комплексно-сопряженные корни вида, а ± р/* (в данном случае введем обозначение мнимой единицы /* = >/—Т). Тогда этим корням соответствуют линейно независимые решения уравнения (21.13) вида.

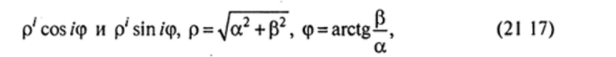
где риф — соответственно модуль и аргумент комплексного корня.

3. Если характеристическое уравнение (21.14) имеет действительный корень q_m кратности г, то ему соответствуют г линейно независимых решений уравнения (21.13) вида

4. Наконец, если характеристическое уравнение (21.14) имеет комплексносопряженный корень (см. п. 2), кратность которого равна г, то ему соответствуют 2 г линейно независимых решений уравнения (21.13) вида.

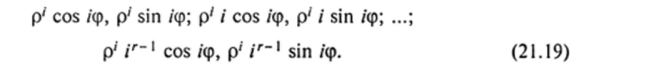
Рассмотрим несколько примеров решения линейных разностных уравнений с постоянными коэффициентами.

Пример 3. Найти flfillirft IVMIIffHMft ПЯ’ШЛГТНПГО УПЯИНРНИЯ.

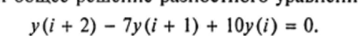aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">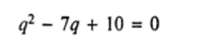

Решение. Это однородное уравнение второго порядка; его характеристическое уравнение имеет простые корми q_x = 2 и q₂ = 5. Согласно п. 1 общее решение данного уравнения имеет вид: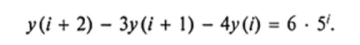

Пример 4. Найти общее решение неоднородного уравнения.

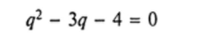
Решение. Соответствующее однородное уравнение имеет постоянные коэффициенты, а его характеристическое уравнение.

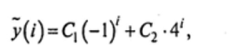
— два простых корня: </, = -1 и q₂ = 4. Следовательно, общее решение однородного уравнения имеет вид: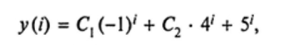

где С, и С₂ — произвольные постоянные.

Одно из частных решений заданного неоднородного уравнения будем искать, сообразуясь с видом правой части: Y (i) = С • 5', где С — постоянная, подлежащая определению. Подставив такое частное решение в исходное разностное уравнение, получаем: С • 5^{/ + 2} — ЗС • 5^{/ + 1} — 4С • 5' = 6 • 5', или 25С -5' - I5C • • 5' - 4С • 5' = 6 • 5¹, откуда С — 1. Таким образом, общее решение заданного уравнения как сумма его частного решения и общего решения однородного уравнения имеет вид: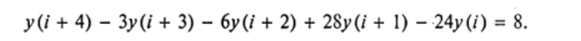

где Cj и С₂ — произвольные постоянные.

Пример 5. Найти общее решение неоднородного уравнения.

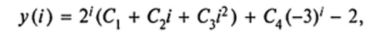
Решение. Это неоднородное уравнение четвертого порядка с постоянными коэффициентами. Найдем его частное решение в виде постоянной величины Y= С; подстановка в уравнение дает: С = -2. Характеристическое уравнение четвертого порядка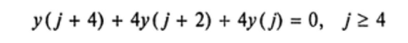

имеет корень q_{ = 2 кратности три и простой корень q₂ = -3. Следовательно, в силу п. 3 общее решение данного уравнения имеет вид:

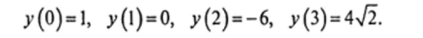
где С, С₂, С₃, С₄ — произвольные постоянные.

Пример 6. Найти решение задачи Коши для уравнения четвертого порядка 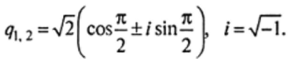с заданными начальными условиями: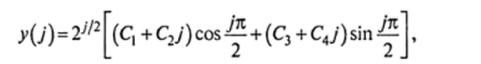

Решение. Характеристическое уравнение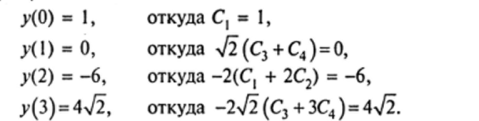

имеет два комплексно-сопряженных корня кратности два каждый:

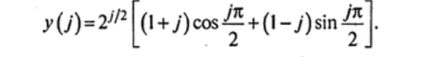
Тогда в соответствии с п. 4 общее решение данного однородного уравнения имеет вид:

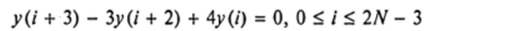
где С, С₂, С_у С₄ — произвольные постоянные.

Теперь найдем частное решение — решение задачи Коши, для чего подставим найденное общее решение в заданные начальные условия. Получаем систему линейных алгебраических уравнений относительно неизвестных величин С, С₂, Су С₄: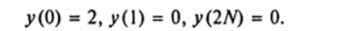

Решая эту систему, находим: С₂ = 1, С₃ = 1, С₄ = -1. Окончательно решение задачи Коши имеет вид:

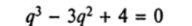
Пример 7. Найти решение краевой задачи для однородного уравнения третьего порядка.

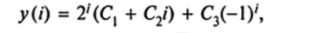
при следующих краевых условиях:

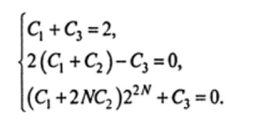
Решение. Характеристическое уравнение.

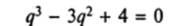
имеет корень <7, = 2 кратности два и простой корень q₂ — -1. Следовательно, общее решение данного уравнения имеет вид:

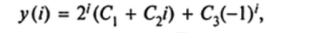
где C_]t Су С₃ — произвольные постоянные. Подставляя это решение в заданные граничные условия, получаем систему трех линейных уравнений относительно указанных постоянных: